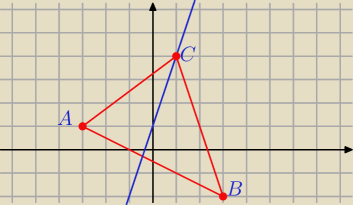
Geometria analityczna Justyna: Pole trójkąta ABC o wierzchołkach A(−3 1) i B(3,−2) jest równe 15. Wierzchołek C należy do prostej o równaniu y= 3x + 1. Oblicz współrzędne wierzchołka C.

5-latek: No to pani Justyno sprawdzimy czy zrobila Pani rysunek do zadania . Pytanie . Ile będzie takich punktów C ?

Justyna: No właśnie nie zrobiłam rysunku, próbowałam rozwiązywać bez rysunku i nic z tego nie wyszło

===: chyba jednak jeden −

Justyna: Wyznaczyłam, że punkt C ma współrzędne (x,3x+1) skoro należy do prostej y= 3x + 1, ale nic mi to nie dało.

===: już nie podpuszczam −

Justyna: Wiesz jak to zrobić?

Janek191: C = ( x , 3 x + 1) → BA = [ −6 , 3 ] → BC = [ x − 3, 3 x + 1 + 2 ] = [ x − 3, 3x +3 ] Pole Δ ABC → → P = 0,5 I det ( BA , BC) I = 0,5 *I −6*( 3 x + 3) − 3*(x − 3) I = = 0,5* I − 18 x − 18 − 3 x + 9 I = 0,5 *I − 21 x − 9 I = I − 10,5 x − 4,5 I = 15 więc x = 1 y = 3*1 + 1 = 4 C = ( 1, 4) ========

Justyna: Pole ze wzoru 1/2 * a * b * sin (a,b) tak?

5-latek:

Justyna: Kurcze, bo tak mi to wyglądało, ale własnie nie pasowało mi to, bo nie mamy podanego kąta. W takim razie nie rozumiem zapisu powyżej. Staram się to zrozumieć, ale nie potrafię

Justyna: I to zadanie ma 2 rozwiązania, bo punkt C może znajdować się jeszcze w 3 ćwiartce.

Janek191:

	13		32
Lub C = ( −		, −		)
	7		7

==============================

Janek191: Jeżeli → v = [ v_x, v_y] → w = [ w_x, w_y ] to → → det ( v , w ) = v_x*w_y − v_y*w_x

5-latek: det to wyznacznik

Justyna: Takiego wzoru nie ma nawet w mojej książce z zakresem rozszerzonym, dlatego nie wiedziałam o co chodzi. A co to jest det ?

Janek191: Wyznacznik . W tym przypadku wyznacznik pary wektorów.

5-latek: Ale jest w tablicach maturalnych

Janek191: To jest bardzo przydatny wzór

Justyna: Właśnie przejrzałam tablice maturalne i znalazłam taki wzór na pole trójkąta P= 1/2 |(x_B−x_A)(y_C−y_A) − (y_B−y_A)(x_C−x_A), ale tego z wektorami nie było. Ale jak podstawię t\do tego wzoru to chyba też będzie dobrze. Zaraz spróbuję

Eta: To jest ten sam wzór! o którym napisał Janek

5-latek: Ale zauważ ze to jest dokładnie to samo co napisał Janek o 21:44

Justyna: No już widzę, ale jestem ślepa... Zmyliło mnie to, że nie było wzoru z tym całym wyznacznikiem 'det', który był wcześniej podany.

Eta: det(→AB, →AC)= |x_B−x_A, y_B−y_A| |x_C−x_A, y_C−y_A| = (x_B−x_A)*(y_C−y_A)−(y_B−y_A)(x_C−x_A)

Justyna: Aaa, czyli o to chodziło. No i teraz wszystko jest jasne Dzięki

Justyna: Właśnie nigdy nie wiedziałam skąd się ten wzór bierze, ale już teraz rozumiem