trójkąt, środek łączący boki trójkąta
maturzystka : hej!
jestem tegoroczną maturzystką, rozwiązuje sobie zadania i tak się zastanawiam, czy środek
łączący środki boków trójkąta zawsze będzie równoległy do podstawy tego trójkąta?
czy ktoś mógłby mi pomóc rozwiać moje wątpliwości ?
27 kwi 19:39
Janek191:
Pewnie chodzi Ci o odcinek ?
27 kwi 19:40
maturzystka : taak! przepraszam pomyliłam się − odcinek łączący środki boków
27 kwi 19:42
maturzystka : czy ktoś się zainteresuje?

27 kwi 19:48
PW: Jest to tzw. powszechnie znany fakt, a wynika z …
27 kwi 19:49
maturzystka : zzz?

27 kwi 19:51
Janek191:
27 kwi 19:51
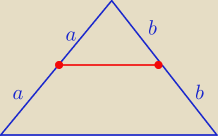
Janek191:
Tales z Miletu

27 kwi 19:52
5-latek: Witam
PW 
Z twierdzenia Talesa .
jest to twierdzenie o,linii srodkowej trojkata
27 kwi 19:53
PR: Jest również równy połowie podstawy

27 kwi 19:55
PW: Z żalem zawiadamiam, że nie z twierdzenia Talesa, lecz z twierdzenia odwrotnego do twierdzenia
Talesa. Nie mamy tu informacji, że proste są równoległe (a takie jest założenie twierdzenia
Talesa). Dlatego
Janek191 podpowiadał młodzieży hasłowo, żeby sama sprawdziła.

27 kwi 19:57
maturzystka :
Przepraszam za małe litery.
Może pokażę zadanie:
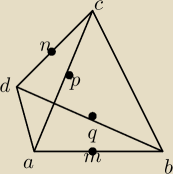
Dany jest czworokąt wypukły ABCD niebędący równoległobokiem. Punkty M, N są
odpowiednio środkami boków AB i CD. Punkty P, Q są odpowiednio środkami przekątnych
AC i BD. Uzasadnij, że MQ jest równoległe do PN.
Wpadłam na pomysł, że odcinek NP jest środkiem łączącym środki ramion trójkąta ADC
oraz, że QM jest odcinkiem łączącym środki ramion trójkąta ADB.
odcinek łączący środki trójkąta jest równoległy do podstawy tego trójkata, a że trójkąty ADC i
ADB mają wspólną podstawę to NP I MQ są równoległe.
czy to jest dobrze?

27 kwi 20:00
maturzystka : prooosze mi pomóc

czy tyle jeśli napiszę to wystarczy ? czy będe jeszcze musiała jakoś udowadniac ze te odcinki
łączace srodki są równoległe do podstaw?
w jaki jeszcze sposób mozna rozwiazac to zadanie?
27 kwi 20:05
PW: Piszesz w rozwiązaniu "Jak wiadomo odcinek łączący środki boków jest równoległy do podstawy".
Twierdzenie jest prawdziwe, znasz je, koniec. Przecież twierdzenia Pitagorasa też nie
dowodzimy za każdym razem, gdy z niego korzystamy.
27 kwi 20:10
maturzystka : dzięki

czy jest ktoś kto potrafi rozwiązać te zadanie w inny sposób?
27 kwi 20:11
maturzystka : haaalooooo! pomoże ktoś?

27 kwi 20:19
PR: O co chodzi?

27 kwi 20:22
maturzystka : w jaki jeszcze sposób mozna rozwiązac to zadanie

27 kwi 20:24




 Z twierdzenia Talesa .
jest to twierdzenie o,linii srodkowej trojkata
Z twierdzenia Talesa .
jest to twierdzenie o,linii srodkowej trojkata


 Przepraszam za małe litery.
Może pokażę zadanie:
Dany jest czworokąt wypukły ABCD niebędący równoległobokiem. Punkty M, N są
odpowiednio środkami boków AB i CD. Punkty P, Q są odpowiednio środkami przekątnych
AC i BD. Uzasadnij, że MQ jest równoległe do PN.
Wpadłam na pomysł, że odcinek NP jest środkiem łączącym środki ramion trójkąta ADC
oraz, że QM jest odcinkiem łączącym środki ramion trójkąta ADB.
odcinek łączący środki trójkąta jest równoległy do podstawy tego trójkata, a że trójkąty ADC i
ADB mają wspólną podstawę to NP I MQ są równoległe.
czy to jest dobrze?
Przepraszam za małe litery.
Może pokażę zadanie:
Dany jest czworokąt wypukły ABCD niebędący równoległobokiem. Punkty M, N są
odpowiednio środkami boków AB i CD. Punkty P, Q są odpowiednio środkami przekątnych
AC i BD. Uzasadnij, że MQ jest równoległe do PN.
Wpadłam na pomysł, że odcinek NP jest środkiem łączącym środki ramion trójkąta ADC
oraz, że QM jest odcinkiem łączącym środki ramion trójkąta ADB.
odcinek łączący środki trójkąta jest równoległy do podstawy tego trójkata, a że trójkąty ADC i
ADB mają wspólną podstawę to NP I MQ są równoległe.
czy to jest dobrze? 
 czy tyle jeśli napiszę to wystarczy ? czy będe jeszcze musiała jakoś udowadniac ze te odcinki
łączace srodki są równoległe do podstaw?
w jaki jeszcze sposób mozna rozwiazac to zadanie?
czy tyle jeśli napiszę to wystarczy ? czy będe jeszcze musiała jakoś udowadniac ze te odcinki
łączace srodki są równoległe do podstaw?
w jaki jeszcze sposób mozna rozwiazac to zadanie?
 czy jest ktoś kto potrafi rozwiązać te zadanie w inny sposób?
czy jest ktoś kto potrafi rozwiązać te zadanie w inny sposób?


