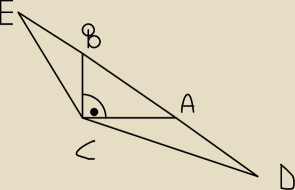
sgjk;o' Tośka: Obwód trójkąta ABC jest równy 2p. |AD|=|AC| i |BE|=|BC|. Wykaż że promień okręgu opisanego na trójkącie ECD jest równy p√2

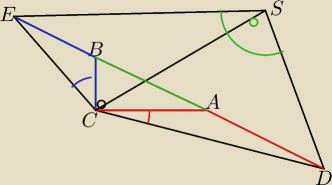
vaultboy: Niech S będzie środkiem okręgu opisanego. Oznaczmy <CBA=a wtedy <CAB=90−a ,bo jest to trójkąt prostokątny <CBE=180−a <CAD=90+a wtedy <BCE=a/2 <ACD=45−a/2 ,bo EBC i CAD są równoramienne. Zatem <ECD=135 ⇒ <ESD=90 oraz ES=SD zatem ΔESD jest połową kwadratu, czyli r=ES=√2ED, ale 2p=czerowny+niebieski+zielony, czyli ED=2p zatem r=2√2p

vaultboy: sry blef w rachunku ED=√2ES stąd r=p√2 przepraszam

Exi: Dlaczego <ESD=90? Z czego to wynika?

vaultboy: bo kąt wklęsły <ESD=270 stopni, gdyż jest on dwa razy większy od kąta wpisanego <ECD, który wynosi 135 stopni

Exi: Faktycznie, zapomniałem o tym. Bez karty wzorów w ręce nie potrafię nawet takich prostych rzeczy ogarnąć Dzięki za wyjaśnienie.