geometria płaska Ola : Na płaszczyźnie zaznaczono n punktów, n≥3, z których dowolne trzy nie są współliniowe. Wyznacz n, wiedząc, że liczba wszystkich odcinków łączących te punkty jest równa a) 21 jak rozwiązać tego typu zadanie z użyciem wzoru n(n−1)/2 ?

J:

	n 2		(n−1)*n
tak .. to 2 elementowe kombinacje ... x =		=
			2

Ola : czyli że co powinnam z tym zrobić będąc w 1 klasie LO ?

Mila: Liczba odcinków:

n 2		n*(n−1)
	=
		2

n*(n−1)
	=21
2

n*(n−1)=42, n∊N₊⇔ 6*7=42 czyli n=?

J: każdy punkt n łączysz z pozostałymi (n −1) punktami ... = n*(n−1) i dzielisz przez 2 , bo para (A,B) = (B,A)

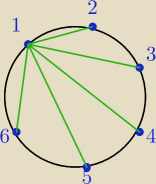
Mila: Masz 6 punktów ; Z jednego punktu możesz poprowadzic 5 odcinków, łączących ten punkt z pozostałymi. Z 6 punktów masz 6*5 odcinków, ale każdy jest liczony dwa razy

6*5
	− liczba wszystkich odcinków, dorysuj do końca to zrozumiesz.
2

Uogólniamy : n− punktów

n*(n−1)
	− liczba wszystkich odcinków łączącyh 6 punktów,z których dowolne trzy nie są
2

współliniowe.