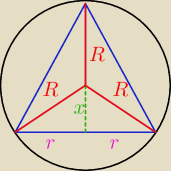
qqq huhuhu: W kulę o promieniu długości R wpisano stożek o maksymalnej objętości. Oblicz objętość tego stożka x²+r²=R² r² = R² − x² H = R+x

	1		1
V =		π(R2−x2)(R+x) =		π(R3+R2x−Rx2−x3)
	3		3

	1
V'(x) =		π(R2−2Rx−3x2)
	3

próbuję wyznaczyć x₁ i x₂,ale nie wychodzi mi. .

huhuhu: dobra znalazłem błąd i mam taki zapis Δ = 16R² √Δ = 4R

	1
x1 =		R
	3

x₂ = −R

Benny: Co nie wychodzi? Δ=16R² √Δ=4R

	2R−4R
x1=
	−6

	2R+4R
x2=
	−4

	1
x1=		R
	3

x₂=−R bierzemy tylko x₁, ponieważ x musi być dodatni

	4
H=		R
	3

	8
r2=		R2
	9

	1		8		4
V=		π*		R2*		R
	3		9		3

	32
V=		πR3 sprawdź
	81

huhuhu: dzięki za wysiłek jak znalazłem błąd to wszystko poszło jak u Ciebie eh..są może jakieś założenia,które muszę napisać?

huhuhu: wszystko poszło jak u Ciebie dzięki za wysiłek. są jakieś założenia do tego zadania,które muszę napisać? oczywiście poza tym,że te wielkości są >0