Największa i najmniejsza wartość funkcji w kwadracie danym równaniem klej: Witam , zadanie brzmi : Znajdź najmniejszą i największą wartość funkcji : f(x,y)=x²+y²−xy w kwadracie : K={(x,y): ]x]+]y]<=1} Wiem jak to zrobić ale mam jeden problem : nie umiem wyznaczyć największych i najmniejszych wartości funkcji na krawędziach tego kwadratu , po proszę o ładne rozpisanie , ja już sobie to rozkminie Pozdrawiam

klej: sorka , kwadrat to |x|+|y|<=1

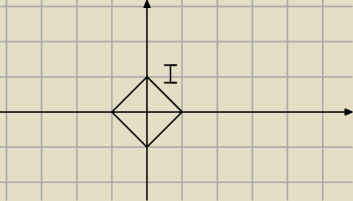
ICSP: Parametryzujemy odcinek I : I = { (t , 1 − t) , 0 ≤ t ≤ 1} i wstawiamy do funkcji : f(I) = t² + (1 − t)² − t(1−t) = ... , 0 ≤ t ≤ 1 Dzięki temu dostałeś funkcję jednej zmiennej i wiadomo co dalej robić. Pozostałe trzy odcinki identycznie : najpierw paramteryzacja a potem szukanie ekstremów w wyznaczonym przedziale.