| 3 | ||
Wyznaczyłem promień | . Potrzebuje jeszcze środka. Pomocy. Wyznacz równanie okręgu | |
| 2 |
 zamowilem już czesc 1 Matura zbior zadań (Podkowa ) i Stachnika na ocene celujaca
Ale powiem Ci z ekoszty wysylki na allegro porazaja
zamowilem już czesc 1 Matura zbior zadań (Podkowa ) i Stachnika na ocene celujaca
Ale powiem Ci z ekoszty wysylki na allegro porazaja 
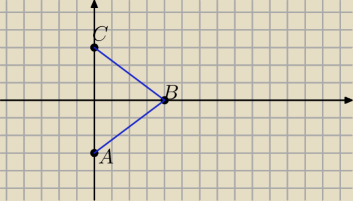 jeśli ma to być geometria ananlityczna to
Z rusunku widać ze mamy już równanie jednej dwusiecznej (czyli x=0
równanie drugiej dwusiecznej otzrzymamy 1. licząc np. składowe wektorow AB i AC
2. majac ich składowe liczymy ich dlugosci
3. ;Liczymy teraz cosinusy kierunkowe αx i αy wektora AB i także cosinusy kierunkowe βx i
βy wektora AC
4. Stad mamy kierunek dwusiecznej kata o wierzchołku A
(αx+βx):(αy+βy)= trzeba policzyć
5. Na podstawie tego piszsemy równanie dwusiecznej
6. Wspolrzedne srodka okręgu wpisanego w ten trojkat to punkt przecięcia obu dwusiecznych .
Koniec zadania
jeśli ma to być geometria ananlityczna to
Z rusunku widać ze mamy już równanie jednej dwusiecznej (czyli x=0
równanie drugiej dwusiecznej otzrzymamy 1. licząc np. składowe wektorow AB i AC
2. majac ich składowe liczymy ich dlugosci
3. ;Liczymy teraz cosinusy kierunkowe αx i αy wektora AB i także cosinusy kierunkowe βx i
βy wektora AC
4. Stad mamy kierunek dwusiecznej kata o wierzchołku A
(αx+βx):(αy+βy)= trzeba policzyć
5. Na podstawie tego piszsemy równanie dwusiecznej
6. Wspolrzedne srodka okręgu wpisanego w ten trojkat to punkt przecięcia obu dwusiecznych .
Koniec zadania  )
.
)
.