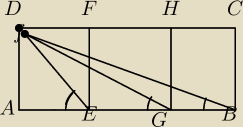
Proszę o pomoc.. Gackt : 1)Prostokąt ABCD jest złożony z trzech kwadratów: AEFD, EGHF i GBCH tak, jak na rysunku. Wykaż że:Uzasadnij, że 90°=∢ AED + ∢AGD + ∢ABD 2)Dwusieczna kąta ACB przecina bok AB tego trójkąta w punkcie D. Oznaczmy długości odcinków AC, BC i DC odpowiednio b,a,d. Wykaż że: d<2ab/(a+b).

pigor: ..., nie wiem na jakim poziomie chcesz rozwiązanie, dlatego np. tak : 1) DE − przekątna kwadratu ADFE o boku a i niech |∡AED|=α, |∡AGD|=β, |∡ABD|=γ, to (*) α+β+γ= 45^o+β+γ = ?

	a
tgβ=		=12, tgγ=13, to ze wzoru na tangens sumy :
	2a

	tgβ+tgγ		12+13
tg(β+γ)=		=		=
	1−tgβtgγ		1−12*13

	3+2
=		=1, zatem β+γ=45o, stąd i z (*)
	6−1

α+β+γ= 45^o, czyli |∡AED|+|∡AGD|+|∡ABD|= 790^o. ... c.n.w.

pigor: ... oczywiście w ostatniej linijce nie 790^o, tylko 90^o.

pigor: ..., no to jeszcze np. tak : zad. 2) niech 2γ − miara kata ACB Δ, to z rysunku zgodnego z warunkami zadania ,masz takie np. równanie : S_ΔACD+ S_ΔBDC= S_ΔABC ⇔ ¹₂bdsinγ+¹₂adsinγ= ¹₂absin2γ ⇔ ⇔ bdsinγ+adsinγ= 2absinγcoγ /:sinγ>0 ⇔ bd+ad= 2abcoγ ⇔

	2ab		2ab
⇔ d(a+b)=2abcosγ ⇒ d =		cosγ i 0<|cosγ|<1 ⇒ d<		. c.n.w.
	a+b		a+b

Gackt : Dzięki