Ostrosłup norek: Krawędź podstawy ostrosłupa prawidłowego trójkątnego ma długość a, natomiast cosinus kąta między jego sąsiednimi ścianami bocznymi jest równy ⁷₁₅. Wyznacz objętość tego ostrosłupa. Wiem, że twierdzenie cosinusów, jednak nie wiem co dalej. Ktoś stwierdził w necie, że "Jest to ostrosłup, w którym krawędź boczna jest 2 razy dłuższa od krawędzi podstawy, to wynika z podanej wartości cosinusa." − ale jak to sprawdzić? Na oko?

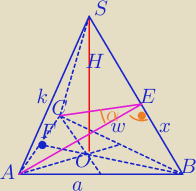
Mila: W ΔACE: a²=w²+w²−2w²*cosα a²=2w²−2w²*cosα a²=2w²*(1−cosα)

	a2		a2		15a2
w2=		=		=
	2*(1−cosα)		7   2*(1− )   15		16

WΔAEB: a²=w²+x²

	15a2
a2−		=x2
	16

1a2
	=x2
16

	a
x=
	4

W ΔAES: k²=w²+(k−x)² Oblicz stąd k k=2a

( ͡° ʖ̯ ͡°): Mila tylko jak z tego obliczyć H?

( ͡° ʖ̯ ͡°): Według mnie należało skorzystać z podobieństwa ΔFOS do ΔFBE

( ͡° ʖ̯ ͡°): A nie przepraszam nie ważne.

( ͡° ʖ̯ ͡°): W sumie twój sposób jest łatwiejszy.

	2
np |AO| =		hp
	3

h_p= wysokość podstawy h_p = a√3/2 i obliczyć H Pitagorasem P_p =U {a² √3}{4}

( ͡° ʖ̯ ͡°):

	a2√3
Pp =
	4