Dany jest trojkat gdzie A (0,0),B(-2,3),C(1,5). Trojkat ten jest: Luna: Dany jest trojkat gdzie A (0,0),B(−2,3),C(1,5). Trojkat ten jest: rownoboczny, prostokatny,roznoboczny czy rozwartokatny?

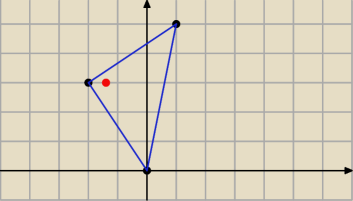
Qulka: prostokątny

Janek191: → AB = [ − 2−0, 3 − 0 ] = [ − 2 , 3 ] więc I AB I = √(−2)² + 3² = √13 → BC = [ 1 − (−2), 5 − 3] = [ 3, 2] więc I BC I = √ 3² + 2² = √13 → AC = [ 1 − 0, 5 − 0 ] = [ 1 , 5 ] więc I AC I = √ 1² + 5² = p[26} Mamy I AB I² + I BC I² = 13 + 13 = 26 = I AC I² czyli Δ ABC jest prostokątny równoramienny. ==================================== II sposób : → BA = [ 2 , − 3] → BC = [ 3, 2] Iloczyn skalarny → → BA o BC = 2*3 + (−3)*2 = 0 więc wektory są prostopadłe czyli boki AB i BC są prostopadłe, co oznacza iż Δ ABC jest prostokątny. ===================================================