Bardzo proszę Madzia: Czy mogłabym jeszcze prosić o pomoc? Mam kilkanaście przykładów do zrobienia na jutro . Czy mógłby ktoś mi pomóc zrobić dla wzoru? Błagam 1. Wyznacz równania stycznych do okręgu x² + y² + 2x − 4y − 4 = 0 prostopadłych do prostej

	1
y=		x + 9
	2

	1
2. Wyznacz równania stycznych do paraboli y =		x2 prostopadłych do prostej y = 3√2 −
	16

	1
		x
	2

	1
3. Wyznacz równania stycznych do paraboli y =		x2 przechodzących przez A(0, −2)
	8

AROB: Pomogę zad.1.

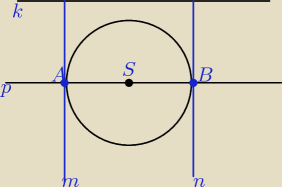AROB: Zad. 1. Z równania okręgu wyznaczamy jego środek i promień: S(a,b) −2a = 2 ⇒ a = −1 −2b = −4 ⇒ b = 2 , czyli S(−1, 2) c = −4, r = √a²+b²−c, r = √1+4+4 = 3

	1
k : y=		x + 9
	2

Styczne m i n są prostopadłe do prostej k, więc ich współczynnik kierunkowy = −2.. Wyznaczam równanie prostej p II k i przechodzącej przez S(−1, 2) : y = ax + b

	1		5
2 =		* (−1) + b ⇒ b =
	2		2

	1		5
Czyli p : y =		x +
	2		2

Punkty styczności A i B należy wyznaczyć z układu równań ( okrąg i prosta p): x² + y² +2x −4y −4 = 0

	1		5
y =		x +
	2		2

Po podstawieniu prostej do okręgu i redukcji otrzymamy równanie kwadratowe: 5x² + 10x − 31 = 0

	−5+6√5		−5−6√5
Δ = 720, √Δ = 12√5, x1 =		, x2 =
	5		5

	3√5+10		−3√5+10
Wtedy: y1=		, y2 =
	5		5

Czyli powstały 2 punkty styczności (okropne!) :

	−5+6√5		3√5+10		−5−6√5		−3√5+10
A(		,		), B(		,		)
	5		5		5		5

Równania stycznych: m : y − y_A = a_m(x − x_A)

	3√5+10		−5+6√5
y −		= −2(x −		)
	5		5

	−5+6√5 + 3√5 + 10		9√5+5
y = −2x +		= −2x +
	5		5

n: y − y_B = a_n(x − x_B) Podstaw analogicznie ( bo cierpliwości mi brakło ).

Eta: AROB .... moja Ty kochana x² +2x +1 −1 +y² −4y +4 −4 −4=0 ( x +1)² +(y−2)² = 9 S( −1,2) r= 3 teraz tak: styczna ma współczynnik kierunkowy a₂= −2 więc piszę równanie stycznej: y= −2x +b przekształacam do : −2x −y +b =0 odległość S od prostej : d= r=3

	I −1*(−2) −1*2 +bI
więc : d=		= 3
	√22+1

I bI= 3√5 => b = 3√5 v b= −3√5 są dwie takie styczne: [C y = −2x +3√5 i y = −2x −3√5 ]]

Eta: pomogę 2/ styczna ma równanie: y = 2x +b bo wsp. kier. a₂ = 2 rozwiązując układ równań prostej i paraboli nałożymy warunek na deltę : Δ= 0 −−− bo maja tylko jeden punkt wspólny zatem: ¹₁₆x² = 2x +b ¹₁₆x²−2x −b =0 Δ= 4 +¹₄b więc Δ=0 <=> ¹₄b +4=0 => b= −16 jest tylko jedna taka styczna : y = 2x − 16 3/ podobnie prosta styczna ma równanie: y= ax +b i A(0,−2) to: −2 = 0*a +b => b = −2 zatem prosta ma równanie: y= ax −2 teraz podobnie jak w zad. 2) ¹₈x² = ax −2 ¹₈x² −ax +2=0 Δ= a² − 1 to Δ=0 <=> a² = 2 => a= 1 v a= −1 są zatem dwie styczne: y= x−2 i y= −x −2 Dobranoc..... miłych snów nie tylko o stycznych