Geometria
Przemysław:
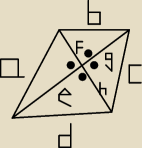
Dany jest czworokat wypukły o nastepujacych własnosciach:
• w czworokat mozna wpisac okrag,
• przekatne czworokata sa prostopadłe.
Dowiesc, ze jedna z przekatnych czworokata dzieli druga na połowy.
No to mam układzik:
| ⎧ | a+c=b+d | |
| ⎜ | f2=b2−g2 | |
| ⎨ | g2=c2−h2 |
|
| ⎜ | h2=d2−e2 | |
| ⎩ | e2=a2−f2 | |
Tylko jak pokazać, że e=g, f=h?
Jakoś z kątami poszaleć?
Będę wdzięczny za pomoc
25 kwi 20:23
Przemysław: .
25 kwi 20:39
ax:
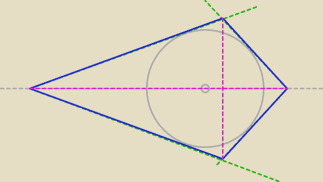
25 kwi 20:54
Przemysław: O
o
Faktycznie, dziękuję.
Tylko jak to teraz wykazać...
25 kwi 20:56
Kacper:
W miarę dobrze kombinujesz. Jeszcze tylko trzeba skorzystać w pewnym miejscu ze wzoru
a
2−b
2=(a+b)(a−b)
25 kwi 21:01
Przemysław: Aha! No może i faktycznie, już działam, dziękuję
25 kwi 21:03
ax:
Z faktu, że w Twój czworokąt można wpisać okrąg wynika wiele rzeczy ... nie tylko równe
sumy długości naprzeciwległych boków ... a w połączeniu z faktem, że przekątne przecinają się
pod kątem prostym ...
25 kwi 21:05
Kacper:
ax nie chciałbym być niegrzeczny, ale twoje posty nic nie wnoszą do tematu. Nie rozumiem
po co się trudzisz?
25 kwi 21:07
Przemysław: Chyba nawet nie trzeba z tego korzystać:
f
2=b
2−c
2+d
2−e
2
b=a+c−d
f
2=a
2+2ac−2ad+c
2−2cd+d
2−c
2+d
2−e
2
f
2=a
2+2ac−2ad−2cd+2d
2
f
2=2a(c−d)−2d(c−d)+a
2−e
2
a
2−e
2=f
2
0=2(a−d)(c−d)
a−d=0 lub c−d=0
a=d lub c=d
Weźmy przypadek a=d, w drugim analogicznie.
Wtedy:
a+c=b+d
c=b
| ⎧ | f2=b2−g2 | |
| ⎜ | g2=b2−h2 | |
| ⎨ | h2=d2−e2 |
|
| ⎩ | e2=d2−f2 | |
b
2−f
2=b
2−h
2
f
2=h
2
f=h lub f=−h, ale f>0 i h>0
Czyli mamy czego chcieliśmy.
@Kacper
A, w którym miejscu to można było zrobić?
25 kwi 21:31
Maniek: f2=b2+c2−(d2−e2)
26 kwi 00:44