wartość bezwględna
tyu:
czy ktoś mógłby mi wytłumaczyć jak to przekształcić
Jeśli x<−2, to wyrażenie I1−Ix+1II jest równe ....
Wiem, że muszę wybrać liczbę z przedziału x<−2, np x=−5 i potem podstawiać.
24 kwi 21:42
tyu: czy to powinno być tak, że
I1−
(−1)(x+1)II wewnętrzny moduł np dla x=−5 jest ujemny, więc go opuszczając, zmieniam
znak w module

czyli mam
I1−(−x−1)II = I1+x+1I= Ix+2I i znów podstawiam np x=−5 i wychodzi mi, że I−3I, czy znów
zmieniam znak, opuszczając moduł
−(x+2)= −x−2

24 kwi 21:49
Eta:
dla x<−2 |x+1| = −x−1
to |1−(−x−1)|= |x+2| to dla x<−2 |x+2|= −x−2
24 kwi 21:49
PW: To taka "wersja dla dzieci".
Jeżeli
(1) x < − 2,
to
x + 1 < − 2 + 1
x +1 < −1,
czyli na pewno (x+1) jest liczbą ujemną, wobec tego badane wyrażenie jest równe
|1 − (− x − 1)| = |2+x| = − x − 2.
Ostatnia równość wynika z (1), gdyż nierówność ta oznacza, że x+2 < 0..
24 kwi 21:52
PW: "wersja dla dzieci" to był komentarz do podstawiania −5 (godz. 21:42).
24 kwi 21:54
Mila:
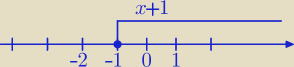
Korzystasz z definicji wartości bezwzględnej.
|x+1|=x+1 dla x+1≥0⇔dla x≥−1
|x+1|=−x−1 dla x<−1
zatem dla x<−2 wyrażenie |x+1| ma wartość −x−1 wtedy mamy taką syuację:
|1−(−x−1)|=|1+x+1|=|x+2|
|x+2|=x+2 dla x≥−2
|x+2|=−x−2 dla x<−2
===============
24 kwi 21:56
tyu: dziękuję wszystkim za pomoc

24 kwi 21:59
Mila:
Witam
Etę i PW, mało potrzebujących pomocy , coś obejrzę w TV.
Dobranoc


24 kwi 22:01
 czyli mam
I1−(−x−1)II = I1+x+1I= Ix+2I i znów podstawiam np x=−5 i wychodzi mi, że I−3I, czy znów
zmieniam znak, opuszczając moduł
−(x+2)= −x−2
czyli mam
I1−(−x−1)II = I1+x+1I= Ix+2I i znów podstawiam np x=−5 i wychodzi mi, że I−3I, czy znów
zmieniam znak, opuszczając moduł
−(x+2)= −x−2 
 Korzystasz z definicji wartości bezwzględnej.
|x+1|=x+1 dla x+1≥0⇔dla x≥−1
|x+1|=−x−1 dla x<−1
zatem dla x<−2 wyrażenie |x+1| ma wartość −x−1 wtedy mamy taką syuację:
|1−(−x−1)|=|1+x+1|=|x+2|
|x+2|=x+2 dla x≥−2
|x+2|=−x−2 dla x<−2
===============
Korzystasz z definicji wartości bezwzględnej.
|x+1|=x+1 dla x+1≥0⇔dla x≥−1
|x+1|=−x−1 dla x<−1
zatem dla x<−2 wyrażenie |x+1| ma wartość −x−1 wtedy mamy taką syuację:
|1−(−x−1)|=|1+x+1|=|x+2|
|x+2|=x+2 dla x≥−2
|x+2|=−x−2 dla x<−2
===============


