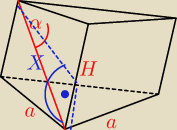
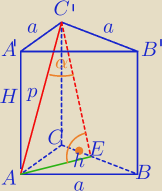
Objętność granistosłupa. Adrian: W graniastosłupie prawidłowym trójkątnym krawędź podstawy ma długość a, a przekątna ściany bocznej tworzy z drugą ścianą boczną kąt α. Wyznacz objętość tego graniastosłupa. Czy tam jest kąt prosty ?

ax: ... przecież tak dobierałeś tą przerywaną na ścianie aby był prosty −

Adrian: upewniam się. I co teraz ? sinα= ^a√3₂/p{a² + H²) ale co dalej ?

Mila:

	a2√3
V=		*H
	4

	a√3
h=
	2

WΔAEC':

	h
sinα=
	p

h=p*sinα

	h
p=
	sinα

	a√3
p=
	2sinα

W ΔACC': p²=H²+a² H²=p²−a²

	a√3
H2=(		)2−a2
	2sinα

	3a2
H2=		−a2
	4sin2α

	3
H2=a2*(		−1)
	4sin2α

	3−4sin2α
H2=a2*
	4sin2α

	a*√3−sin2α
H=
	2sinα

Rozwiązanie istnieje dla takiego α∊(0,90^o), że (3−4sin²α)>0 Rozwiąż ten warunek ......

	a3√3*√3−4sin2α
V=
	8sinα

===================