Zbadac ciaglosc funkcji w punkcie
Krzysiek: f(x)=x2 dla x ≤ 0
−1/x dla ≥0
24 kwi 12:50
J:
popraw treść
24 kwi 12:53
Krzysiek: lim x2 = 0
lim −1/x = −∞
coś takiego?
24 kwi 12:54
Krzysiek: nie mam jak poprawić treści
24 kwi 12:56
Krzysiek: f(x)=x2 dla x ≤ 0
−1/x dla x ≥ 0
24 kwi 12:56
J:
a w jakim punkcie badasz
24 kwi 12:59
J:
nie mośe być: x ≥ 0 oraz x ≤ 0 ... któraś musi być ostra
24 kwi 13:00
Krzysiek: więc tak będzie
f(x)=x2 dla x < 0
−1/x dla x ≥ 0
i jak to zrobić? wydaje mi się że będzie lim −1/x = −∞ a w tym pierwszym +∞?
24 kwi 13:06
J:
lim f(x)x→0− = 0
lim f(x)x→0+ = − ∞
f nie jest ciągła w x = 0
24 kwi 13:08
Krzysiek: możesz to narysować?
24 kwi 13:11
J:
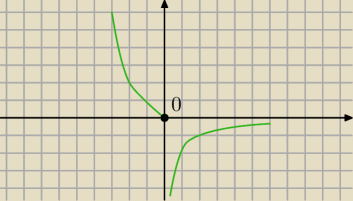
24 kwi 13:13
Krzysiek: lim f(x)x→0− = 0
nie rozumiem zbytnio tego
24 kwi 13:24
J:
to oznacza,że liczymy granicę przy x → 0 od lewej strony ( granica lewostronna)
24 kwi 13:25
Krzysiek: a co z x < 0, to nie powinno tego ograniczyć?
24 kwi 13:28
Saizou :
x
2 dla x≤0
F(x)=
Aby funkcja F(x) była ciągła w punkcie a potrzeba i wystarczy, aby zachodziła równość
F(a)=lim
x→a−F(a)=lim
x→a+F(a)
Zbadajmy ciągłość w punkcie a=0
F(0)=0
2=0
lim
x→0+F(x)=lim
x→0+x
2=0
0=0≠−
∞
zatem funkcja F(x) jest nieciągła w punkcie a=0
24 kwi 13:28
J:
@
Saizou ... odwrotnie zmierzanie x → 0

24 kwi 13:33
Saizou :
Tak, ale wartości się nie zmienią, zasugerowałem się pierwszym wpisem
Krzyśka i nie
odczytałem go do końca, ale bądź co bądź dla funkcji którą ja mam zdefiniowaną jest dobrze

24 kwi 13:35
J:
a ponadto ... podane przez Ciebie warunki nie są wystarczające

24 kwi 13:35
Saizou :
To jaki wg Ciebie jest warunek wystarczający ?
24 kwi 13:40
Krzysiek: na tym rysunku nie powinno być pustej kropki?
24 kwi 13:40
J:
Aby funkcja była ciągła w pukcie x0 muszą byc spełnione 3 warunki:
1) funkcja musi posiadać wartość w punkcie x0
2) musi posiadać granicę w punkcie x0 ( lewostronna = prawostronnej)
3) granica w punkcie x0 musi być równa wartości funkcji w punkcie x0
24 kwi 13:44
J:
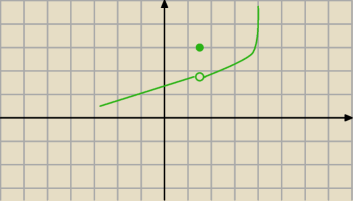
Twoje warunki są spełnione ... a funkcja nie jest ciągła

24 kwi 13:47
J:
OK ... teraz widzę,że napisałeś: F(a) .. .czyli posiada wartość

24 kwi 13:49
Saizou :
a co ja napisałem
"Aby funkcja F(x) była ciągła w punkcie a potrzeba i wystarczy, aby zachodziła równość
F(a)=limx→a−F(a)=limx→a+F(a)"
F(a) wartość funkcji w punkcie a
limx→a−F(a),limx→a+F(a) posiadanie granicy
F(a)=limx→a−F(a)=limx→a+F(a) równość wartości i granicy
24 kwi 13:50
J:
OK ... ja to przeoczłem

24 kwi 13:51
Krzysiek: czemu ta funkcja ma być ciągła? myślałem że mam to tylko zbadać a może wyjść inna
24 kwi 13:51
Saizou :
Funkcja, którą napisałeś jest nieciągła w xo=0
Jak masz polecenie zbadać ciągłość (nieciągłość), to masz stwierdzić czy funkcja jest ciągła
czy nieciągła
24 kwi 13:53
Saizou :
a te moje rozważania tyczyły się ogólnego rozrachunku o ciągłości
24 kwi 13:54




 Twoje warunki są spełnione ... a funkcja nie jest ciągła
Twoje warunki są spełnione ... a funkcja nie jest ciągła 

