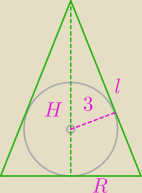
Stożek, kula, optymalizacja zozol: Zbadaj, jaką wysokość powinien mieć stożek opisany na kuli o promieniu 3, aby jego objętość była najmniejsza. Oblicz jaki procent objętości tego stożka stanowi objętość kuli. Teoretycznie powinienem wiedzieć jak to zrobić: r − 3 R − promien podstawy stożka H wysokosc stożka l − tworząca stożka ze wzorow na pole:

r(2l + 2R)		HR
	=
2		2

6(l + R) = HR tu moge wstawić za l √H² + R² i wyznaczyć R w zależnosci od H, tylko nie jestem w stanie... Nie chce mi nic wyjsc... Pomoże ktoś? Może powinienem innym sposobem?

zozol: prosze

ax:

R		3
	=		⇒ 3l=RH−3R
l		H−3

l=√H²+R² 3√H²+R²=RH−3R 9H²+9R²=R²H²−6R²H+9R² ⇒ R²H²−6R²H−9H²=0

	6R2
R2H−6R2−9H=0 H(R2−9)=6R2 ⇒ H=
	R2−9

	1		6R2		2πR4
Vs=		πR2*		=
	3		R2−9		R2−9

	8πR3(R2−9)−4πR5
Vs'=
	(R2−9)2

V_s'=0 4πR⁵−72πR³=0 ⇒ R²−18=0 R=3√2 itd

zozol: bardzo dziekuje