trójkąt Archy: w trójkącie ABC dane są: AB=7 BC=3 CA=8. Oblicz pole powierzchni całkowitej i objętość bryły powstałej w wyniku obrotu trójkąta ABC wokół boku BC.

	13
myślałem żeby skorzystać z twierdzenia cosinusów i wyszedł mi cosBAC=		no ale nie wiem
	14

jak to dalej pociągnąć

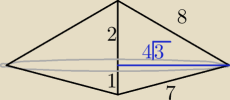Qulka: dwa Pitagorasy

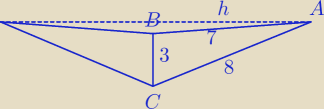Janek191: Mamy h² + x² = 7² h² + ( x + 3)² = 8² −−−−−−−−−−− h² + x² = 49 h² + x² + 6 x + 9 = 64 −−−−−−−−−−−−−−− odejmujemy stronami 6 x + 9 = 64 − 49 = 15 6 x = 15 − 9 = 6 x = 1 === h² = 49 − 1² = 48 = 16*3 h = 4√3 ======= Zatem w bryle obrotowej r = h = 4√3

	1
V =		π *( 4√3)2 * 3 = 48 π
	3

==========================

Archy: dziękuję