Matura Blue: Czy do tej nierówności |2cos4x|>1 jest też poprawne takie rozwiązanie

	−π		πk		π		πk		π		πk		π		πk
x∊(		+		,		+		) U (		+		,		+		)
	12		2		12		2		6		2		3		2

Blue: Bo w odpowiedziach, mam inaczej, ale mnie się wydaje, że na jedno wyjdzie, więc się upewniam

Ajtek: To pokaż odpowiedzi, pomyślimy

Blue: http://i61.tinypic.com/2le5g95.png proszę

Ajtek: Nie otwiera mi się to coś . Napisz odpowiedź ze zbioru

Blue:

	−π		πk		π		πk
(		+		,		+		)
	12		4		12		4

Ajtek: No to chyba jednak nie to samo .

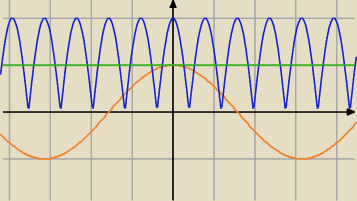
Ajtek: Tak wygląda "wykres". Na zielono y=1, na pomarańczowo f(x)=cosx, dla pomocy przy określaniu ułamków π

Blue: Jak to nie ? Jesteś pewien?

Ajtek: Ty masz sumę dwóch przedziałów.

Blue: No tak, ale czy w efekcie nie jest to to samo, podstaw sobie np. 1 za k w tym 1

Ajtek: Dobra: dla k=1.

	π		π*1		π		π*1
−		+		≠−		+
	12		2		12		4

Blue: Dobra, niech Ci będzie, dziękuję

Ajtek: Widzisz, gdzie masz błąd?

( ͡° ʖ̯ ͡°):

Blue: No tam mniej więcej, tzn jakbym narysowała wykres, to pewnie bym dobrze zrobiła, ale ja myślałam, że na to trzeba spojrzeć tak cos4x>1/2 i cos4x<1/2, ale najwyraźniej coś mi się pokręciło

Blue: tak*

Ajtek: No coś się pokićkało Tobie . Spokojnej!

Ajtek: Idąc Twoim tokiem myślenia to: |2cos4x|>1 2cos4x>1 u 2cos4x<−1 cos4x>0,5 u cos4x<−0,5 itd.... .

( ͡° ʖ̯ ͡°): @Ajtek (✌ ﾟ ∀ ﾟ)☞