a
msp: Dla jakich wartości parametru a równanie
x2 + y2 − 2ax − a2 + 2a = 0
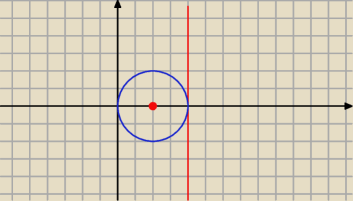
opisuje okrąg styczny do prostej x=4?
x2 − 2ax +a2 −2a2 + y2 +2a=0
(x−a)2+y2 = 2a2 − 2a
więc S=(a,0)
|4−a| = √2a2 − 2a czy to jest poprwane założenie do obliczenia tej wartości?
23 kwi 18:52
PW: A zagwarantowałeś sobie, ze "kandydat na r2" jest dodatni?
23 kwi 19:32
Janek191:
( x − a )
2 − a
2 + ( y − 0)
2 −a
2 + 2a = 0
( x − a)
2 + ( y − 0)
2 = 2 a
2 − 2a
więc
a = p{2 a
2 − 2 a) i 2a
2 −2 a >0
a
2 = 2 a
2 − 2a
a
2 −2 a = 0
a*( a − 2) = 0
a = 0 − odpada lub a = 2 wtedy r
2 = 2 a
2 − 2a = 2*4 − 2*2 = 4
r = 2
Równanie okręgu:
( x − 2) + ( y − 0)
2 = 4
=================
Odp. a = 2
24 kwi 08:48
ola:
25 kwi 20:50
ola: pole powierzchni bocznej stożka jest 2 razy większe od pola podstawy , a promień podstawy
ma długość 6cm oblicz tangens kąt nachylenia tworzącej stożka do podstawy oraz
objętość bryły.
25 kwi 20:55
Kacper:
Załóż nowy temat.
25 kwi 21:02
Janek191:
r = 6
P
b = 2 P
p
więc
π r l = 2 π r
2 / : π r
2
l = 2 r
l = 2*6 = 12
h
2 = l
2 − r
2 = 12
2 − 6
2 = 144 − 36 = 108 = 36*3
h = 6
√3
| | h | | 6√3 | |
tg α = |
| = |
| = √3 ⇒ α = 60o |
| | r | | 6 | |
| | 1 | | 1 | |
V = |
| Pp *h = |
| π r2 * h = ... |
| | 3 | | 3 | |
25 kwi 21:02