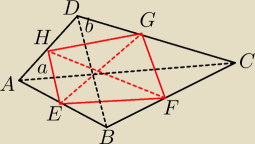
www kluski: W czworokącie wypukłym ABCD punkty E,F,G i H są odpowiednio środkami boków AB,BC,CD i DA oraz |EG| = |FH|.Wykaż,że pole tego czworokąta jest niewiększe niż

1		a+b
	(		)2,gdzie a i b oznaczają długości przekątnych czworokąta.
2		2

wiem tyle,że EFGH jest prostokątem i nie mam pomysłu co zrobić

Tadeusz: ... a skąd wniosek, że EFGH jest prostokątem?

Mila: 1) Czworokąt EFGH jest równoległobokiem ( to wynika z tw. Talesa) 2) Ten równoległobok jest prostokątem, bo ma równe przekątne.

	1
3) |HG|=|EF|=		a (0dcnek łączący środki boków Δ jest równoległy do trzeciego boku i równy
	2

połowie tego boku)

	1
4)|GF|=|HE|=		b
	2

	1		1		1
5) PEFGH=		a *		b=		a*b
	2		2		4

6) Wykaż, że zachodzi nierówność :

1		1		a+b
	a*b≤		*(		)2 dla każdego a, b>0
4		2		2

kluski: bo E, F, G, H to środki boków czworokąta,EF i GH równoległe są do AC,również FG i EH do DB i te odcinki są równe połowie przekątnym czworokąta(czyli równoległobok),a że EG = HF to znaczy,że EFGH jest prostokątem coś w tym stylu..

kluski: dzięki Milu

Mila: