pole trapezu olle: Pole trapezu równoramiennego opisanego na okręgu o promieniu √2 wynosi 6√2. Wyznacz długości boków tego trapezu.

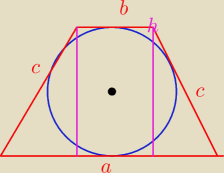
Janek191: h = 2 r = 2√2 P = 0,5*( a + b)*h = 0,5*(a + b)*2√2 = (a + b)*√2 = 6√2 więc a + b = 6 ⇒ b = 6 − a

	a − b		a − 6 + a
x =		=		= a − 3
	2		2

Janek191: 2 c = a + b = 6 c = 3 ==== h² + x² = c² (2√2)² + ( a − 3)² = 9 8 + a² − 6 a + 9 = 9 a² − 6 a + 8 = 0 Δ = 36 − 4*1*8 = 4 √Δ = 2

	6 − 2
a =		= 2 − odpada
	2

lub

	6 + 2
a =		= 4
	2

============== b = 6 − 4 = 2 =========