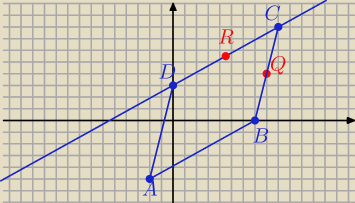
Wyznacz współrzędne wierzchołków Kukumorek: Punty P, Q i R są odpowiednio środkami boków AB, BC i CD równoległoboku ABCD. Wyznacz współrzędne wierzchołków równoległoboku jeżeli:

	9		11
a) wektor AB=[9,5], Q(8,4), R(		,		)
	2		2

	3		9
b) wektor AB=[1,5], wektor AD=[−2,6], P(		, −		)
	2		2

c) wektor AB=[8,−4]  wektor AC=[14,2], P(6,−3)

Maxxx: Dolaczam sie do prosby o rozwiazanie

Janek191: → AB = [ 9, 5] więc

	5
a = tg α =
	9

Prosta CD

	5		11
y =		x + b przechodzi przez R = (U{9}[2} ,		)
	9		2

wiec

11		5		9
	=		*		+ b
2		9		2

b = 3

	5
y =		x + 3
	9

→ → → RC = 0,5 DC = 0,5 AB

	9		11		9
[ x3 −		, y3 −		] = [		,U{5}[2}]
	2		2		2

x₃ = 9 y₃ = 8 C = ( 9, 8 ) ========= D = ( x₄, y₄} → → DC = AB [ 9 − x₄, 8 − y₄] = [ 9, 5] 9 − x₄ = 9 i 8 − y₄ = 5 x₄ = 0 i y₄ = 3 D = ( 0, 3) ======== B = ( x₂, y₂ ) Q = ( 8, 4) jest środkiem odcinka BC , więc

x2 + 9		y2 + 8
	= 8		= 4
2		2

x₂ + 9 = 16 y₂ + 8 = 8 x₂ = 7 y₂ = 0 B = ( 7, 0 ) ========= A = ( x₁, y₁) więc → AB = [ 7 − x₁, 0 − y₁] = [ 9, 5] 7 − x₁ = 9 − y₁ = 5 x₁ = − 2 y₁ = − 5 A = ( − 2, − 5) ==========

Janek191: Ten fragment dotyczący prostej CD nie jest potrzebny

Kukumorek: Dziękuję bardzo