prosta i okrąg
maciek: Prosta o równaniu x+y=r jest styczna do okręgu o równaniu x2+y2=r. Uzasadnij że wówczas r=2
22 kwi 23:17
Bogdan:
Sprawdź zapis treści zadania
23 kwi 00:24
23 kwi 00:26
Qulka:
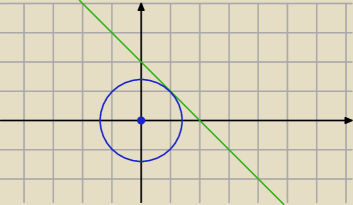
23 kwi 00:31
Bogdan:
na tym rysunku r ≠ 2, ale r = √2
23 kwi 00:33
Qulka: na tym rysunku r=2 więc promień okręgu = √2, bo tam (wzór) nie ma r2 tylko samo r
23 kwi 00:36
pigor: ..., no bo maciek po prostu nie wie, że w równaniu
okręgu jest x2+y2=r2, a nie r i to nie r=2, tylko r2=2 i tyle .
23 kwi 00:39
Bogdan:
Jeśli x
2 + y
2 = r, a nie x
2 + y
2 = r
2, to promień tego okręgu ma długość
√r.
y = r − x i x
2 + (r − x)
2 = r ⇒ 2x
2 − 2rx + r
2 − r = 0
Założenie: Δ = 0 i r > 0:
Δ = 4r
2 − 8r
2 + 8r = 0 ⇒ −4r
2 + 8r = 0 ⇒ −4r(r − 2) = 0
r = 2 lub r = 0 sprzeczne
Nawyk widzenia w równaniu okręgu r
2 spowodował wątpliwości

23 kwi 00:52

