funkcja
student:
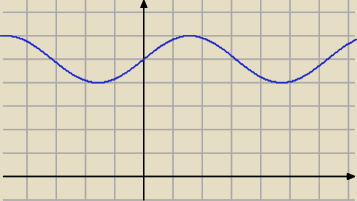
y=5x+sinx
Wyznaczyć przedziały monotoniczności tej funkcji.
22 kwi 23:08
student: ?
22 kwi 23:13
Bogdan:
a student zna pojęcie pochodnej funkcji?
22 kwi 23:16
PW: Normalnie − pochodną liczysz i oceniasz gdzie dodatnia.
22 kwi 23:16
student:
wyznaczyłem pochodną y=5x−cosx
pochodna y=5+sinx
i dalej nie wiem co ?
23 kwi 10:05
J:
pochodna: y = 5 + cosx , teraz ustal przedziały , gdzie pochodna jest dotatnia , a gdzie
ujemna
23 kwi 10:08
5-latek: y'=(5x)'+(sinx)'
y'= 5+cosx
23 kwi 10:11
student:
funkcja jest y=5x−cos(x)
pochodna y=5x+sinx
Ale jak ustalić te przedziały, jak ją narysować ?
23 kwi 10:12
student:
hmm ?
23 kwi 10:14
J:
student ... oprzytomniej i nie mieszaj ... pochodna: y = sinx + 5 ... masz jej wykres ...
jaki ma znak ta pochodna
23 kwi 10:17
student:
pochodna>0
23 kwi 10:18
J:
dla jakich x ?
23 kwi 10:22
student:
dla x∊R ?
23 kwi 10:23
student: ?
23 kwi 10:29
J:
OK ... skoro w pochodna jest dotania w całej dziedzinie, to w całej dziedzinie funkcja jest ...
?
23 kwi 10:30
student:
Funkcja jest rosnąca

Masz jeszcze chwilkę ?
23 kwi 10:35
J:
co jest ?
23 kwi 10:36
student:
Mam jeszcze kilka zadań i potrzebuję pomocy

23 kwi 10:41
student:
. Naszkicuj wykres funkcji i omów jej własności (dziedzina, monotoniczność, ekstrema
lokalne, granice na końcach przedziałów określoności, miejsca zerowe)
a) f(x)=ex
D=R
Brak miejsc zerowych
funkcja rosnąca dla x∊R
granice na końcach przedziałów ?
ekstrema lokalne:brak
?
23 kwi 10:43
J:
limx→ − ∞ex = 0
limx→ + ∞ex = + ∞
23 kwi 10:45
student:
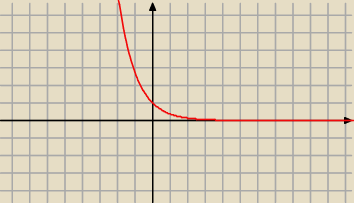
b) f(x)=e
−x
D=R
Brak miejsc zerowych
funkcja malejąca
Brak ekestremów lokalnych
granice na krańcach przedziału ?
lim
x→∞e
−x=0
lim
x→−∞e
−x=
∞
?
23 kwi 10:56
J:
tak
23 kwi 10:57
student:
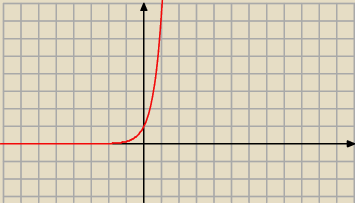
c) f(x)=e
2x
D=R
Miejsca zerowe:brak
ekstremum lokalne:brak
funkcja rosnąca dla x∊R
lim
x→∞e
2x=
∞
lim
x→−∞e
2x=0
?
23 kwi 11:10
J:
tak
23 kwi 11:11
student:
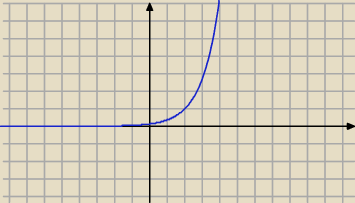
d) ) f(x)=e
x−2
D=R
Miesjca zerowe:brak
ekstremum lokalne brak
funkca rosnąca dla x∊R
lim
x→∞e
x−2=
∞
lim
x→−∞e
x−2=0
?
23 kwi 11:12
J:
tak
23 kwi 11:13
student:
Teraz zaczną się moje kłopoty
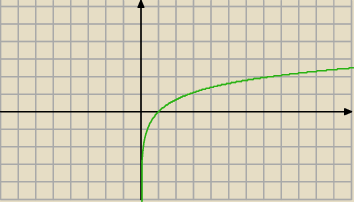
e) f(x)=lnx
Miejsca zerowe (1,0)
Ekstremum lokalne ?
Funkcja rosnąca
i granice też problem
23 kwi 11:16
J:
patrz na wykres:
D = R+
Miejsce zerowe: x = 1
Funkcja rosnąca
Brak ekstremów
Granice: − ∞ , + ∞
23 kwi 11:19
student:
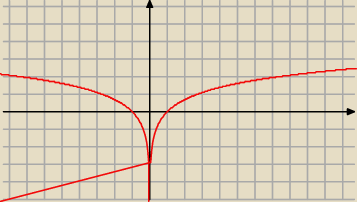
f) f(x)=ln|x|
Miejsca zerowe (−1,0) (,1,0)
Ekstremum brak ?
Funkcja jest ?
granica ?
23 kwi 11:39
J:
monotoniczna w przedziałach
23 kwi 11:41
student:
rosnąca od (0,∞)
Malejąca (−∞,0)
ekstrema i granice ?
23 kwi 11:47
J:
a jak myslisz ?
23 kwi 11:48
student:
nie wiem właśnie

23 kwi 11:51
J:
przecież masz wykres przed oczami
23 kwi 11:52
student:
x→−∞=∞
x→∞=∞
ekstremum lokalne ?
23 kwi 11:53
J:
ekstremum brak ... a co gdy x → 0 i co z asymptotami ?
23 kwi 11:55
student:
x→0=−∞
23 kwi 11:57
student:
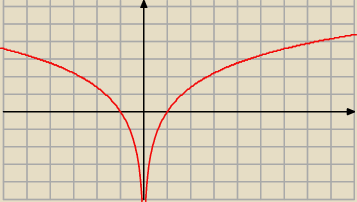
g) f(x)=lnx
2
malejąca od (−
∞,0)
rosnąca od (0,
∞)
miejsca zerowe (−1,0) (1,0)
ekstremum brak ?
23 kwi 11:59
student: ?
23 kwi 12:06
student: up up
23 kwi 12:14
student: ?
23 kwi 12:27
J:
Dziedzina ?
Asymptoty ?
23 kwi 12:29
student:
D=R
asymptota x=0
23 kwi 12:32
student:
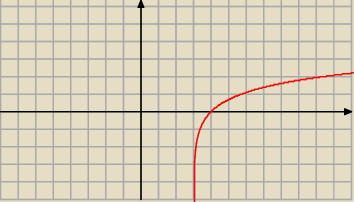
h) ln(x −3) .
D=R
MZ=(4,0)
funkcja rosnąca
ekstremum lokalne brak
lim
x→∞=
∞
lim
x→−∞=−
∞
23 kwi 12:35
student: ?
23 kwi 12:41
J:
zła dziedzina
asymptota ?
23 kwi 12:43
J: 12:32 ... też zła dziedzina
23 kwi 12:45
student:
12:32 zła dziedzina ?
12:35 asymptota x=3
Dziedzina też nie wiem
23 kwi 12:46
J:
12:32 .. przecież x = 0 nie należy do dziedziny
12:35 .. warunek: x − 3 > 0 ⇔ x > 3 , czyli: D = ?
23 kwi 12:49
student:
12:32 D=R\{0}
12.35 D=(3.∞)
23 kwi 12:50
J:
tak
23 kwi 12:51
student:
ok, jeszcze dwa zadania dosłownie
Dla jakich wartości parametru a funkcja f (x) x3−ax2+5x ma w punkcie x =11 lokalne
ekstremum? Jakie to jest ekstremum? Wyznacz przedziały monotoniczności tej funkcji.
23 kwi 12:55
J:
licz pochodną
23 kwi 12:57
student:
f'(x)=3x2−2ax+5 tam ba być w punkci x=1 jak coś
23 kwi 13:02
J:
teraz warunek: f'(1) = 0
23 kwi 13:04
student:
3−2a+5=0
2a=8
a=4
f(x)=x3−4x2+5x
liczę pochodną i określam monotoniczność ?
23 kwi 13:21
J:
pochodna: f'(x) = 3x2 − 8x + 5
teraz naszkicuj pochodną ... z wykresu odczytamy ekstrema i monotoniczność
23 kwi 13:23
student:
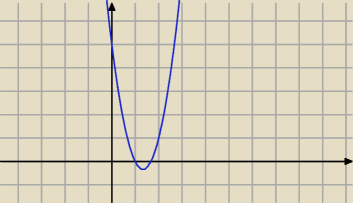
23 kwi 13:29
J:
gdzie się pochodna zeruje ?
23 kwi 13:30
23 kwi 13:43
J:
dobra , tam mogą być ekstrema ( to warunek konieczny) ..
czy pochodna zmienia znak w tych punktach ( warunek wystarczający) , a jeśli tak, to jak ?
23 kwi 13:46
student:

23 kwi 13:50
J:
nie ... (−∞,1) f'(x) > 0 ... funkcja jest ...?
(1;3.5) f'(x) < 0 ... funkcja jest.. ?
(3.5;+∞) f'(x) >0 funkcja jest ?
23 kwi 13:53
J:
tam ma byc oczywiście 5/3 , anie 3.5
23 kwi 13:54
student:
malejąca
rosnąca
malejąca
jak ekstremum teraz odszukać ?
23 kwi 13:58
J:
| | 5 | |
skup się: −∞ ... rosnąca ... 1 ..... malejąca ... |
| .... rosnąca .... + ∞ |
| | 3 | |
wnioski ?
23 kwi 14:00
student:
podałem przedziały monotoniczniści
ekstremum brak ?
23 kwi 14:06
J:
rusz głową ... jesli funkcja rośnie do x = 1 , a potem maleje , to dla x = 1 osiaga ?
23 kwi 14:08
J:
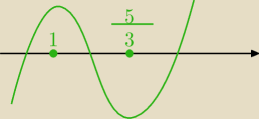
widzisz to ?
23 kwi 14:10
student:
dla x=1 osiąg maximum lokalne
23 kwi 14:12
23 kwi 14:13
student:
minimum lokalne.
czy przedziały montonicznośc dobrze wyznaczyłem ?
23 kwi 14:17
J:
patrz na wykres ... gdzie rosnie, gdzie maleje
23 kwi 14:18
student:
ale który wykres, bo są dwa wykresy
23 kwi 14:19
J:
wykres funkcji ( bo to jej monotonicznośc badasz ) ... wykres ( przyblizony) 14:10
23 kwi 14:20
23 kwi 14:23
J:
nareszcie
23 kwi 14:23
student:
Dzięki

23 kwi 14:30
 hmm ?
hmm ?
 Masz jeszcze chwilkę ?
Masz jeszcze chwilkę ?

 b) f(x)=e−x
D=R
Brak miejsc zerowych
funkcja malejąca
Brak ekestremów lokalnych
granice na krańcach przedziału ?
limx→∞e−x=0
limx→−∞e−x=∞
?
b) f(x)=e−x
D=R
Brak miejsc zerowych
funkcja malejąca
Brak ekestremów lokalnych
granice na krańcach przedziału ?
limx→∞e−x=0
limx→−∞e−x=∞
?
 c) f(x)=e2x
D=R
Miejsca zerowe:brak
ekstremum lokalne:brak
funkcja rosnąca dla x∊R
limx→∞e2x=∞
limx→−∞e2x=0
?
c) f(x)=e2x
D=R
Miejsca zerowe:brak
ekstremum lokalne:brak
funkcja rosnąca dla x∊R
limx→∞e2x=∞
limx→−∞e2x=0
?
 d) ) f(x)=ex−2
D=R
Miesjca zerowe:brak
ekstremum lokalne brak
funkca rosnąca dla x∊R
limx→∞ex−2=∞
limx→−∞ex−2=0
?
d) ) f(x)=ex−2
D=R
Miesjca zerowe:brak
ekstremum lokalne brak
funkca rosnąca dla x∊R
limx→∞ex−2=∞
limx→−∞ex−2=0
?
 Teraz zaczną się moje kłopoty
e) f(x)=lnx
Miejsca zerowe (1,0)
Ekstremum lokalne ?
Teraz zaczną się moje kłopoty
e) f(x)=lnx
Miejsca zerowe (1,0)
Ekstremum lokalne ?
 f) f(x)=ln|x|
Miejsca zerowe (−1,0) (,1,0)
Ekstremum brak ?
Funkcja jest ?
granica ?
f) f(x)=ln|x|
Miejsca zerowe (−1,0) (,1,0)
Ekstremum brak ?
Funkcja jest ?
granica ?

 g) f(x)=lnx2
malejąca od (−∞,0)
rosnąca od (0,∞)
miejsca zerowe (−1,0) (1,0)
ekstremum brak ?
g) f(x)=lnx2
malejąca od (−∞,0)
rosnąca od (0,∞)
miejsca zerowe (−1,0) (1,0)
ekstremum brak ?
 h) ln(x −3) .
D=R
MZ=(4,0)
funkcja rosnąca
ekstremum lokalne brak
limx→∞=∞
limx→−∞=−∞
h) ln(x −3) .
D=R
MZ=(4,0)
funkcja rosnąca
ekstremum lokalne brak
limx→∞=∞
limx→−∞=−∞


 widzisz to ?
widzisz to ?
