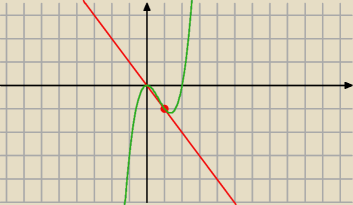
równania stycznej student: Równanie stycznej w punkcie x₀=1 f(x)=x³−2x² f(x)'=3x²−4x f'(1)=−1 f(1)=−1 y=−(x−1)−1 y=−x ?

J: tak

Mila: Dobrze.

student: moge jeszcze wrzucic kilka zadań ? juto mam kolokwium

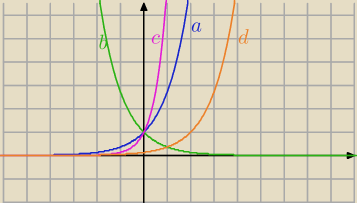
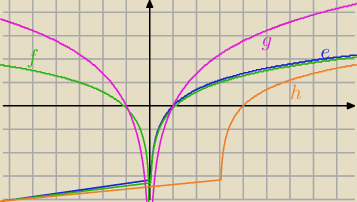
student: 2.Naszkicuj wykres funkcji i omów jej własności (dziedzina, monotoniczność, ekstrema lokalne, granice na końcach przedziałów określoności, miejsca zerowe): a) f(x)=e^x b) f(x)=e^−x c) f(x)=e^2x d) f(x)=e^x−2 e) f(x)=lnx f) f(x)=ln|x| g) f(x)=lnx² h) f(x)=ln(x−3)

student: ?

student: n

Qulka:

student: Qulka a pomożesz z resztą ?

Qulka:

Qulka: te skośne to błąd programu

student: ?

Qulka: w czym problem jeszcze?

student: w dalszej części polecenia.

J: przecież masz gotowe wykresy ... więc na ich podstawie omawiaj własności

Qulka: obrazek 1 dziedzina x∊R, monotoniczność rosnące ( poza b) ona jest jak widać malejąca), ekstrema lokalne: brak granice na końcach przedziałów określoności: jak widać 0 dla −∞ oraz ∞ dla ∞ poza przykładem b) który ma odwrotnie miejsca zerowe: brak

student: Qulka będziesz za 30 minut jeszcze ? te zadania już zrobiłem z J

Qulka: obrazek 2 dziedzina x∊R\{0} dla f) i g) , x>0 dla e) ; x>3 dla h) monotoniczność rosnące w D e) i h) dla x>0 f) i g) , dla x<0 f) i g) malejące ekstrema lokalne: brak granice na końcach przedziałów określoności: jak widać zazwyczaj −∞ dla 0 oraz ∞ dla ∞ oraz w f) i g) ∞ dla −∞ miejsca zerowe: −1 (f,g) 1 (e,f,g) 4 h)

Qulka: za 5 min wychodzę będę za 2−3h