Granice Rafal: lim x x−>3− 9−x² oczywiście pomiędzy x, a 9−x² jest ułamek, a trójka leci po minusach, moim zdaniem to będzie wyglądało tak, że lim 3 = −~~ x−>3− 0− A w odpowiedziach jest, że ma wyjść plus, pomocy

Rafal: Wybaczcie za jakość zapisu

J: jeśli x → 3 od lewej strony to mianownik zmierza do zera po wartosciach dodatnichi i licznik zmierza po dodatnich, czyli: lim = + ∞

Rafal: x −> 3− minusa nie uwzględniłeś

J: zapis: x → 3⁻ oznacza,że x zmierza do 3 od lewej strony

Rafal: czyli liczby te mogą być zarówno dodatnie, jak i ujemne, czyż nie?

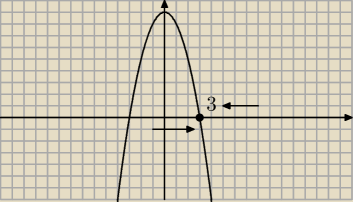
J: popatrz na rysunek ... jeśli x zmierza do 3 od lewje strony , to wyrażenie : 9 − x² zmierza do zera po wartościach dodatnich i odwrotnie

Rafal: Mhm, a mógłbyś jeszcze przedstawić swoją tezę na tym przykładzie? lim x x−>1+ x²−4x+3

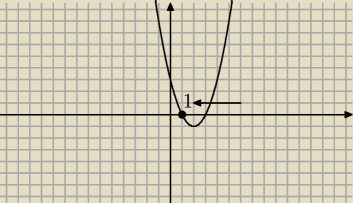
J: x → 1 od prawej strony, czyli mianownik jest ujemny, a licznik dodatni: lim = − ∞

Rafal: Czyli, jakby nie patrzyć, w każdym przypadku, kiedy np. x−>1+, to lim=−~~, a x−>1−, to lim=+~~ racja?

J: to zależy od tego jak się "zachowuje" mianownik

Rafal: A mógłbyś podać przykład, aby obalić moją teorię?

J:

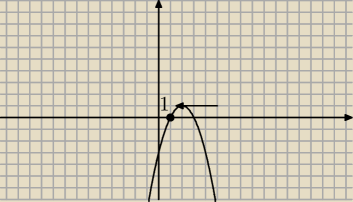
	x
limx→1+		= + ∞ ( bo mianownik zmierza do zera po wartościach
	−x2 + 4x − 3

dodatnich)

J: ale ... lim_x→1⁻ = − ∞

Rafal: Wymyśliłem znacznie łatwiejszy sposób, jeżeli mamy, jak w tym przypadku x−>1+, to pod x wstawiamy liczbę większą od jedynki, a później tylko formalność, zebrać znaki z licznika i mianownika ;>