symetryczna moneta lw: Rzucamy symetryczna moneta do momentu otrzymania pierwszego orla. Jakie jest prawdopodobienstwo, ze wykonamy parzysta liczbe rzutow? Moim zdaniem pytanie troche zle sformulowane − ale jest, to musze rozwiazac. Wiec rozwiazanie takie mam: 1/2⁽2n) ktore uniezaleznia rozwiazanie od jakiegos n, co moim zdaniem jest bledem. Jak to rozwiazac?

PW: Nie jest źle sformułowane, ino przestrzeń zdarzeń ma nieskończenie wiele elementów. Nie można stosować twierdzenia zwanego klasyczną definicją prawdopodobieństwa.

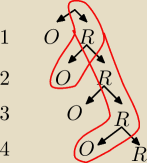
Jacek: A − zdarzenie polegające na wykonaniu parzystej liczby rzutów monetą do momentu otrzymania pierwszego orła

	1
Prawdopodobieństwo wyrzucenia w jednym rzucie reszki: pr =
	2

	1
Prawdopodobieństwo wyrzucenia w jednym rzucie orła: po =
	2

n − numer rzutu P(A) = p_o*p_r + p_o*p_r³ + p_o*p_r⁵ + p_o*p_r⁷ + ......+p_o*p_rⁿ⁻¹ Traktując iloczyn p_o*p_r jako pierwszy wyraz ciągu geometrycznego nieskończonego, zaś p_r² jako iloraz ciągu, możemy P(A) obliczyć jako sumę nieskończonego ciągu geometrycznego o liczbie wyrazów n/2, ale chyba to nic specjalnie nie zmienia. Iloraz ciągu: |p_r²|<1

	1   4		1
P(A) =		=
	1   1−   4		3

lw: Dzieki Jacek, tez doszedlem juz do tego wyniku sumujac 1/2^2k po k