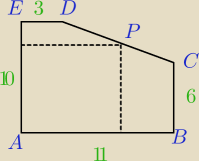
Optymalizacja, blacha zozol: Z kawałka blachy należy wyciąć prostokąt o największym polu, w taki sposóbm jak zostało to pokazane na rysunku (wierzchołek P prostokąta ma należeć do krawędzi CD). Znajdź wymiary tego prostokąta. Robiłem już kilka razy ciągle nie wychodzi... Odp. 11x6

zozol: ktoś? jakas podpowiedz?

Mariusz: Rozpatrz pole powierzchni prostokąta jako funkcję Uzależnij ją od jednego argumentu (chyba że miałeś ekstrema funkcji wielu zmiennych) Policz maksimum tej funkcji (pochodna równa zero , jeżeli w otoczeniu punktu podejrzanego o extremum pochodna zmienia znak z + na − to w tym punkcie jest maksimum)

Marcin: również mam problem z tym zadaniem, pomoże ktoś

Pytający: P(t)=(3+(11−3)*t)*(10−(10−6)*t), t∊<0,1> P(t)=(3+8t)(10−4t)=−32t²+68t+30 // wymiary: (3+8t)x(10−4t) P'(t)=−64t+68>0 dla t∊<0,1> ⇒ P(t) osiąga maksimum dla t=1, (3+8*1)x(10−4*1)=11x6