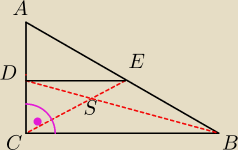
spr tost : Dany jest trójkąt prostokątny ABC,w którym kąt C jest prosty,|CA|=2√2 i |CB|=2. Wykaż,że środkowe BD i CE tego trójkąta są do siebie prostopadłe. a Pitagorasa |AB| = 2√3 tak samo |DB| = √6 CE = AE = EB CD = DA z podobieństwa trójkątów DCB i ABC

CB		DE
	=		⇒ |DE| = 1
DC		AD

trapez DECB jest prostokątny z trójkątów CSB i DES :

CB		DE
	=
CS		SE

2		1
	=
CS		SE

2SE = CS CS + SE = CE 2SE + SE = CE 3SE = √3

	√3
SE =
	3

	2√6
podobnie obliczam SB =
	3

SE² + SB² = EB²

	√3		2√6
(		)2 + (		)2 = {√3)2
	3		3

3		24
	+		= 3
9		9

27
	= 3
9

3 = 3

Bombek12345: na poczatku chyba błąd DE = 2 bo 2/√2=DE/√2 czyli DE= 2

tost :

	CB		DE
oj, chodziło mi o		=
	AC		AD