:D
matma!: sposród ostrosłupów prawidłowych trójkatnych, w których suma długości promienia okregu
opisanego na podstawie ostrosłupa i długosci wysokości tego ostrosłupa jest równa 24, wybrano
ten którego objetość jest najwieksza i przecięto go płaszczyzną prostopadłą do podstawy i
zawierającą odcinek łączący środki dwóch krawędzi podstawy. oblicz pole otrzymanego przekroju.
bardzo prosze o pomoc

22 kwi 12:34
Janek191:
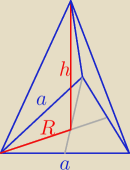
R + h = 24
| | 2 | | 2 | | √3 | | √3 | |
R = |
| hp = |
| a |
| = a |
| |
| | 3 | | 3 | | 2 | | 3 | |
więc
| | √3 | | √3 | |
a |
| + h = 24 ⇒ h = 24 − a |
| |
| | 3 | | 3 | |
22 kwi 13:18
matma!: a jak bedzie wyglądac ten przekrój?
22 kwi 13:26
Janek191:
| | 1 | | 1 | | a2 √3 | | √3 | |
V = |
| Pp*h = |
| * |
| *( 24 − a |
| ) = |
| | 3 | | 3 | | 4 | | 3 | |
więc
| | a2 | | a | | a | |
V' (a) = 4√3 a − |
| = a*( 4 √3 − |
| ) = 0 ⇔ |
| = 4 √3 ⇔ a = 16√3 |
| | 4 | | 4 | | 4 | |
oraz
więc
V''( 16
√3) = 4
√3 − 8
√3 < 0 zatem objętość ostrosłupa jest największa ,gdy
a = 16
√3
−−−−−−−−−
wtedy
−−−−−−−−−−−−−−−−−−−
22 kwi 13:31
Janek191:
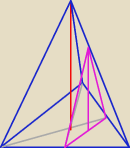
22 kwi 13:36
Janek191:
a' = 0,5 a = 8
√3
Mamy
| 8 | | 16 | | 12*8 | |
| = |
| ⇒ h' = |
| = 6 |
| h' | | 12 | | 16 | |
Pole przekroju:
P = 0,5 a'*h' = 0,5*8
√3*6 = 24
√3
==========================
22 kwi 13:42
matma!: dzieki

22 kwi 13:55

 R + h = 24
R + h = 24

