nierówność pulikowski: Proszę o sprawdzenie cos²x + 2sin²x + 4cosx + 3 ≥ 0 cosx=t t²+2(1−t² ) + 4t + 3 ≥ 0 −t² + 4t + 5 ≥ 0 Δ=36, √Δ=6 t₁ = 5 t₂ = −1 Wyrażenie jest większe od zera dla t ∊ <−1; 5>, jednakże cosx przyjmuje wartości od −1 do 1, więc muszę zawęzić mój przedział do <−1;1> Finalnie x∊R

Ajtek: Generalnie żadnego błędu nie widzę. Ja bym dał założenie jeszcze na starcie: cosx=t i t∊<−1;1> w tym właśnie miejscu!

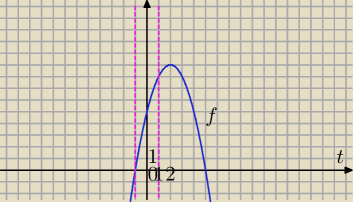
Mila: f(t)=−t²+4t+5 i t∊<−1,1> t_w=2∉<−1,1>⇔ f(t) jest w tym przedziale rosnąca f(−1)=−1−4+5=0 wartość najmniejsza f(t) dla t∊<−1,1> f(1)=−1+4+5=8 wartość najwieksza f(t) dla t∊<−1,1> Zw=<0,8>⇔cos²x + 2sin²x + 4cosx + 3 ≥ 0 dla x∊R