 Z urny,w której znajdują się 3 kule białe i 2 czarne,wybieramy losowo trzy kule,a następnie
rzucamy symetryczną sześcienną kostką do gry tyle razy,ile wylosowaliśmy białych kul.
Oblicz prawdopodobieństwo tego,że otrzymamy co najmniej raz sześć oczek na kostce.
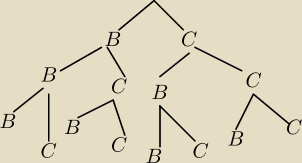
więc z drzewka obliczam prawdopodobieństwo wyciągnięcia 3,2,1 kul/kuli białych/białej.
B − biała
Z urny,w której znajdują się 3 kule białe i 2 czarne,wybieramy losowo trzy kule,a następnie
rzucamy symetryczną sześcienną kostką do gry tyle razy,ile wylosowaliśmy białych kul.
Oblicz prawdopodobieństwo tego,że otrzymamy co najmniej raz sześć oczek na kostce.
więc z drzewka obliczam prawdopodobieństwo wyciągnięcia 3,2,1 kul/kuli białych/białej.
B − biała
| 3 | 2 | 1 | 2 | 3 | 1 | |||||||
B1 = | * | * | + | * | * | + | ||||||
| 5 | 4 | 3 | 5 | 4 | 3 |
| 2 | 1 | 18 | 3 | ||||
* | *1 = | = | |||||
| 5 | 4 | 60 | 10 |
| 3 | 2 | 2 | 3 | 2 | 2 | |||||||
B2 = | * | * | + | * | * | + | ||||||
| 5 | 4 | 3 | 5 | 4 | 3 |
| 2 | 3 | 2 | 6 | ||||
* | * | = | |||||
| 5 | 4 | 3 | 10 |
| 1 | ||
B3 = ... | ||
| 10 |
| 1 | ||
teraz dla B1 rzucamy raz kostką więc prawdopodobieństwo wynosi | ||
| 6 |
| 25 | 11 | |||
P(B2)' = | ⇒ P(B2) = | |||
| 36 | 36 |
| 91 | ||
P(B3) = | ||
| 216 |
| 3 | 1 | 6 | 11 | 1 | 91 | |||||||
P(A)= | * | + | * | + | * | = | ||||||
| 10 | 6 | 10 | 36 | 10 | 216 |
| 595 | 119 | ||
= | |||
| 2160 | 432 |