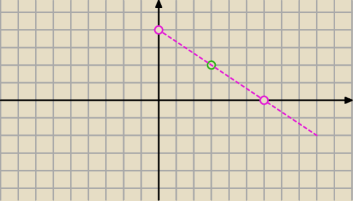
Geometria Karol: Bardzo potrzebuje pomocy z tym zadankiem ! Dany jest punkt P(3,2) znaleźć rownanie prostej przechodzącej przez Punkt P i odcinającej na dodatnich pol osiach układu współrzędnych odcinki OA i OB takie,ze pole trojkata AOB jest równe 12

Tadeusz:

Karol: Tadeuszu... Nadal nie wiem jak się za to zabrać

Tadeusz: Jak wszystko w matematyce możesz policzyć różnymi "ścieżkami" Pokażę Ci nietypową bo rzadko "odwiedzaną"−

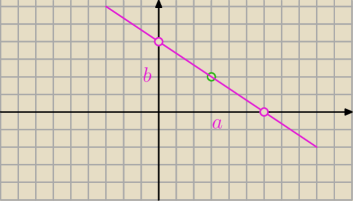
Tadeusz: Prosta odcina na osiach odcinki a i b Fakt, że w treści zadania podano, iż chodzi o odcinki osi nie zmusza nas do zabawy z modułami.

	1
Zauważ, że		ab=12 ⇒ ab=24 ⇒ b=24/a
	2

Teraz równanie prostej w postaci odcinkowej

	x		y		x		y		24x+a2y
		+		=1 ⇒		+		=1 ⇒		=1
	a		b		a		24/a		24a

24x+a²y=24a i do tego równania podstawiamy współrzędne punktu P 72+2a²−24a=0 a²−12a+36=0 ⇒ (a−6)²=0 a=6 b=4 i wszystko jasne−

Tadeusz: ... w drugiej linijce miało być "iż chodzi o dodatnie części osi"

Tadeusz: Dziękuję karolku −:(