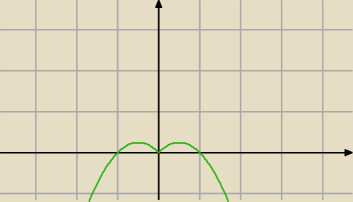
Aksjomat X YushokU: ↑↑↑do zadania 2↑↑↑ Witam, Mam pytanie odnośnie arkusza. Dzisiaj trafił się bardzo łatwy, jednak się zastanawiam nad zadaniami, bo np. tam gdzie mam stronę do dyspozycji, ja mam zadanie rozwiązane w dwie linijki i nie za bardzo wiem, jak je przedłużyć . Zad.1 Funkcja f określona jest wzorem f(x)=sinx+cosx a)Zapisz wzór tej funkcji w postaci iloczynowej.

	π		π		π
f(x)=√2(sinxcos		+cosxsin		)=√2sin(x+		)
	4		4		4

b)Wyznacz zbiór wartości funkcji f. Zw∊<−√2,√2> No i to tyle z mojego rozwiązania. Zadanie jest na 5 punktów! Zad.2 Wyznacz ekstrema funkcji f(x)=|x|+x² Oczywiście nie zauważyłem skrótu i robiłem rozbijając funkcję na dwa przypadki 1.x<0 f'(x)=−1−2x

	−1		1
fmax=f(		)=
	2		4

2.x≥0 f'(x)=1−2x

	1		1
fmax=f(		)=
	2		4

Teraz po wyznaczeniu gdzie funkcja rośnie, gdzie maleje rysuje jej wykres i stwierdzam, że jest nieciągła w x=0 Sprawdzam jej wartość w tym punkcie i stwierdzam, że f_min=f(0)=0 Dobrze? Bo w drugiej części bazowałem na wykresie Z góry dzięki za odpowiedzi

J: a dlaczego uważasz,że jest nieciągła w zerze ?

YushokU: Przepraszam,błąd. Nie jest nieciągła, ale nie ma pochodnej..

Mila: W punktach zmiany wzoru liczysz pochodną z definicji.

Mila: Jeśli jest potrzebna.