pochodna + optymalizacyjne
Mikołaj: Bardzo proszę o pomoc
Na paraboli o równaniu y=x2 znajdź taki punkt P aby kwadrat odległości punktu A=(3, 0) od
punktu P był najmniejszy z możliwych
20 kwi 14:24
J:
P(x,x2) d = √(3−x)2 +(0−x2)2 ... i szukasz minimum
20 kwi 14:26
Mikołaj: po wyliczeniu wychodzi mi d=9−6x i z tego pochodna to −6... coś chyba nie tak

20 kwi 14:39
Mila:
|PA|2=(3−x)2+x4
|PA|2=9−6x+x2+x4
f(x)=9−6x+x2+x4
f'(x)=4x3+2x−6
f'(x)=0 ⇔
4x3+2x−6=0,
w(1)=4+2−6=0
Zbadaj czy w x=1 jest minimum f(x), zostawiam to dla Ciebie.
P=(1,1)
20 kwi 17:53
/_/_/\_\/_/\_\/_/\_\_\: 4x
3+2x−6=y nie ma minimum

21 kwi 00:23
/_/_/\_\/_/\_\/_/\_\_\: pomyłka zaraz poprawie
21 kwi 00:27
/_/_/\_\/_/\_\/_/\_\_\:
f'(x)=x
4+x
2 − 6x+9 = 2(x−1)(2x
2−4x+6)
2(x−1)(2x
2−4x+6) = 0
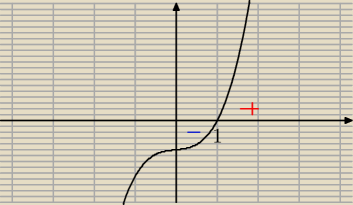
Ma tylko jedno miejsce zerowe dla x=1. Rysujemy wykres, współczynnik przy największym x jest
nie parzysty więc zaczynamy od dołu.
Pochodna zmienia znak z − na + więc w tym miejscu jest minimum.
21 kwi 00:35


 f'(x)=x4+x2 − 6x+9 = 2(x−1)(2x2−4x+6)
2(x−1)(2x2−4x+6) = 0
Ma tylko jedno miejsce zerowe dla x=1. Rysujemy wykres, współczynnik przy największym x jest
nie parzysty więc zaczynamy od dołu.
Pochodna zmienia znak z − na + więc w tym miejscu jest minimum.
f'(x)=x4+x2 − 6x+9 = 2(x−1)(2x2−4x+6)
2(x−1)(2x2−4x+6) = 0
Ma tylko jedno miejsce zerowe dla x=1. Rysujemy wykres, współczynnik przy największym x jest
nie parzysty więc zaczynamy od dołu.
Pochodna zmienia znak z − na + więc w tym miejscu jest minimum.