Prawdopodobieństwo
Polityk: Z urny, w której znajduje się 6 kul białych i 3 czarne losujemy dwie kule. z pozostałych kul
losujemy jedną. Oblicz prawdopodobieństwo tego, że wylosowana kula będzie biała.
Mógłby ktoś powiedzieć jak to zrobić drzewem?
20 kwi 12:53
J:
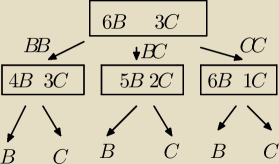
20 kwi 13:01
J:
| | 6*5 | | 3 | | 6*3 | | 2 | | 3*2 | | 1 | |
P(C) = |
| * |
| + |
| * |
| + |
| * |
| |
| | 9*8 | | 7 | | 9*8 | | 7 | | 9*8 | | 7 | |
20 kwi 13:05
Jacek: Tylko żeby pamiętać BC liczyć jako BC i CB
20 kwi 13:05
Jacek: Albo:
| 6*5 | | 3 | | 2*6*3 | | 2 | | 3*2 | | 1 | |
| * |
| + |
| * |
| + |
| * |
| |
| 9*8 | | 7 | | 9*8 | | 7 | | 9*8 | | 7 | |
albo
20 kwi 13:11
Polityk: Obliczyliście prawdopodobieństwo czarnej (a w zadaniu jest biała) w każdym razie odejmując ten
| | 14 | |
wynik od 1 wychodzi |
| po skróceniu, i też zresztą mi tak wyszło jak sobie wszystko |
| | 21 | |
| | 20 | |
rozrysowałem, problem jest jednak taki że odpowiedź to |
| |
| | 21 | |
20 kwi 15:13
Polityk: Ale jak tak patrzę to chyba dobrze policzyliśmy i jest błąd w odpowiedzi, jak myślicie? Ktoś
może sprawdzić na drugą rękę?
20 kwi 15:26
20 kwi 15:29
Jacek: 14/21=2/3 jest OK, faktycznie liczyliśmy dla czarnej na końcu
20 kwi 15:30
