2
Ja: Zadanie 2
Wyznacz równania stycznych do okręgu o równaniu x2+y2−4x+2y+1=0 , równoległych do osi
odciętych układu współrzędnych.
Moze ktos sprawdzic?
obliczylem:
(x−2)2+(y−1)2=4
s=(2,1) r=2
I tutaj nie wiedzialem jak sie za to zabrac wiec opisalem slownie:
Styczne do okregu bedace jednoczenie rownoleglymi do osi odcietych ukladu wspolrzednych sa
prostymu o zerowych wspolczynnikach kierunkowych, więc sa stale.Przedstawiaja sie nastepujaco:
y=0*a+b=b
Punkty styczne do okregu sa oddalone o 2 wartosci od jego drugiej wspolrzednej. Więc: y=1+2=3
lub y=1−2=−1
19 kwi 22:46
Eta:
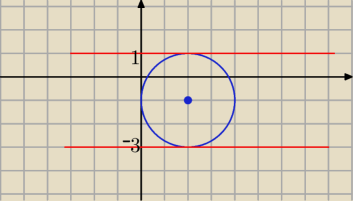
S(2,
−1) r=2
styczne ∥ OX :
y=1 , y= −3
19 kwi 22:53
Qulka:
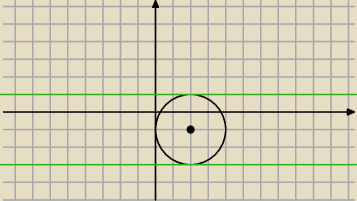
19 kwi 22:55
Eta:

19 kwi 22:55
Ja: Rozumiem ze moj tok rozumowania byl poprawny.
19 kwi 22:57
 S(2, −1) r=2
styczne ∥ OX : y=1 , y= −3
S(2, −1) r=2
styczne ∥ OX : y=1 , y= −3

