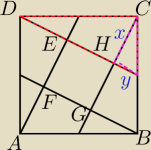
qwerty grzanka: Wierzchołki kwadratu ABCD połączono ze środkami jego boków (zobacz rysunek) i otrzymano w ten sposób mniejszy kwadrat EFGH. Oblicz, jaki jest stosunek obwodów kwadratów ABCD i EFGH. z tego trójkąta czerwonego mam

a2
	+ a2 = c2
4

5a2
	= c2
4

√5a
	= c
2

a		x
	=
√5a     4		a     2

	2a√5
x =
	5

tak kombinować?

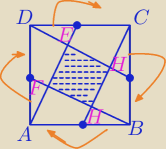Mila: P_ABCD=5*P_EFGH

PABCD
	=5=k2
PEFGH

k=√5 Stosunek obwodów kwadratów ABCD i EFGH=√5

grzanka: dziękuję a czy można w ten sposób :

	a√5
zaznaczony 'x' na rysunku równa się
	5

	a√5		a2
czyli pole EFGH wynosi (		)2 =
	5		5

pole ABCD a²

PABCD		a2		5
	=		= a2*		= 5
PEFGH		a2     5		a2

k² = 5 k = √5 ?

Mila: Tak.