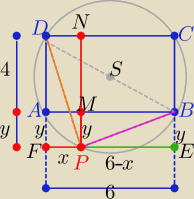
 |PM|=|BE|=y , |PN|=4+y=|DF| , |PF|=x , |PE|=6−x
Mamy wykazać,że :
|PM|2+|PN|2+|PE|2+|PF|2= |DB|2= 62+42=52
Z tw. Pitagorasa
w ΔPFD i ΔPEB i ΔBPD ( jest też prostokątny ... dlaczego?
|PN|2+|PF|2=|PD|2 i ||PE|2+|BE|2= |PB|2 i |PD|2+|PB|2=|DB|2=52
i mamy tezę ................
|PM|=|BE|=y , |PN|=4+y=|DF| , |PF|=x , |PE|=6−x
Mamy wykazać,że :
|PM|2+|PN|2+|PE|2+|PF|2= |DB|2= 62+42=52
Z tw. Pitagorasa
w ΔPFD i ΔPEB i ΔBPD ( jest też prostokątny ... dlaczego?
|PN|2+|PF|2=|PD|2 i ||PE|2+|BE|2= |PB|2 i |PD|2+|PB|2=|DB|2=52
i mamy tezę ................

