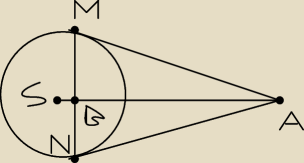
 Na okręgu o promieniu r wybrano punkty M i N w ten sposób, że proste AM i AN są styczne do
okręgu. Punkt B jest punktem wspólnym odcinka MN i prostej łączącej A ze środkiem S tego
okręgu. Wykaż, że |SA| · |SB| = r2.
Na okręgu o promieniu r wybrano punkty M i N w ten sposób, że proste AM i AN są styczne do
okręgu. Punkt B jest punktem wspólnym odcinka MN i prostej łączącej A ze środkiem S tego
okręgu. Wykaż, że |SA| · |SB| = r2.
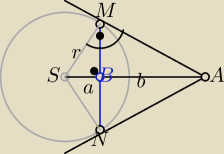 |SB|=a, |BA|=b |SA|=a+b
Z podobieństwa trójkątów SAM i SBM z cechy (kkk)
|SB|=a, |BA|=b |SA|=a+b
Z podobieństwa trójkątów SAM i SBM z cechy (kkk)
| r | |SB| | |||
= | ⇒ r2= |SA|*|SB| | |||
| |SA| | r |