prawdopodobieństwo Marta: A, B są zdarzeniami losowymi zawartymi w Ω. Wykaż, że jeżeli P(A)=0,8 i P(B)=0,7, to P(A'∩B)+P(A∩B')≤0,5 Doszlam do momentu 0,5≤P(A∩B) i nie wiem co dalej, mogę to pomnożyć? Proszę o pomoc, z góry dzięki

Marta: Pomoże ktoś?

pigor: ... , dobrze ... doszłaś, a więc jeszcze raz, a widzę to np. tak :: P(AUB)=P(A)+P(B)−P(A∩B) = 0,8+0,7−P(A∩B) ≤ 1, stąd (*) −P(A∩B) ≤− 0,5 ; także P{AUB)= P(A'∩B)+P{A∩B')+P{A∩B) ≤1, jako suma prawdopodobieństw 3−ech zbiorów (zdarzeń) rozłącznych (wykluczających się), to stąd i z (*) P(A'∩B)+P{A∩B') ≤1−P{A∩B)=1−0,5=0,5 .c.n.w. ...

Marta: Dziękuję a gdyby tak dojść do postaci P(A∪B)≤1 to też byłoby dobrze, czy to jest zawsze prawdziwe?

Mila: Zawsze. https://matematykaszkolna.pl/strona/1018.html

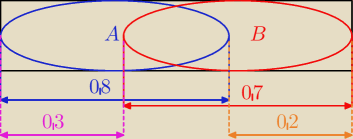
Gustlik: Najlepiej to rozpisał pigor, mozna do tego dowodu pomóc sobie powyższym rysunkiem. Na rysunku widać, że jeżeli P(AUB)=1, to P(A'∩B)+P(A∩B')=0,2+0,3=0,5. Jezeli będziemy "przesuwać" zbiór B w lewo, w stronę zbioru A, czyli P(AUB)≤1, to oba te prawdopodobieństwa bedą maleć, czyli P(A'∩B)+P(A∩B')≤0,5. Z takiego rysunku mozna dojść łatwo do metody pigora.