Prosze o rozwiązania Majjjka: 1 . Udowodnij, że jeżeli b ⁄= 0 i a ⁄= −b , a/b * a/a+b = a/b − a/a+b . Prosze o pomoc. 2. Suma log9 27 + 1 9jest równa 3.Ciąg (an) określony jest wzorem an = (2n − 9)2 − 25 , gdzie n ≥ 1 . Liczba ujemnych wyrazów tego ciągu jest równa 4. Prosta y = mx + 3 tworzy z dodatnimi półosiami układu współrzędnych trójkąt o polu 7. Wyznacz m . Prosze o pomoc.

5-latek: w zadaniu nr 1 brakuje czegos nr 2 = 0,5*3log₃3+19= policz nr 3 rozwiąż nierownosc (2n−9)²−25<0 i pamiętaj z e n∊N₊ Na razie rozwiąż to

Majjjka: Kurde pomyliłam się w drugim zadaniu. Powinno byc log9 27 + 1

Majjjka: Jak poprawiłam ten log to wynik wyszedł mi 3 ,czy dobrze ?

5-latek:

	1
Masz wzor logan bm=		*mloga b
	n

	1
log9 27= log32*33=		*3*log33+1=
	2

Majjjka: Zad. 3 ( 4n2− 36n + 81) − 25 < 0 ?

5-latek: Skoncz to drugie zadanie najpierw

Majjjka: 1/2 * 3log 1+1 na razie jest ok?

Majjjka: Wyszedł mi wynik 5/2 ok ?

5-latek: powinno być tak

1
	*3*1+1= bo log33=1 ze wzoru loga a=1
2

5-latek: Ale wynik masz dobry

Majjjka: 1/2 * 3 log3 3 +1 = 3/2 log 1+1 ?

Majjjka: Ok,dziekuje

5-latek: Teraz następne 4n²−36n+81−25<0 dalej to uprość

Majjjka: 4n2 − 36n + 56 < 0 / 4 n2 − 8n + 14 < 0 i z tego delte ?

Majjjka: Delta wyszła mi zero i rozwiązanie wyszło mi 4,5

5-latek: 4*9=36 a nie 4*8

Majjjka: Zle spojrzałam. Rozwiązanie wyszło mi 4.

5-latek: zle n²−9n+14<0 Δ= b²−4*a*c=

5-latek: Δ=(−9)²−4*1*14= 81−56=

Majjjka: x1 = −4 i x2 = 13

Majjjka: kurde zle...

Majjjka: x1 =2 i x2 = 7

Majjjka: xe ( 2,7 ) dziekuje.

5-latek: < nie> Δ=25 to √Δ= √25=5

	−b−√Δ
n1=		= licz
	2a

	−b+√Δ
n2=		= licz
	2a

nie liczysz po x_ach tylko po n_ach

Majjjka: n1 = 9−5 / 2 = 4/2 = 2 n2= 9+5/2 = 7

Majjjka: i dalej zle ?

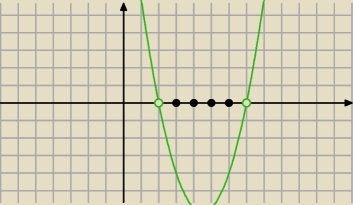
5-latek: Godzina 14:50 to nie jest koniec zadania bo my mamy policzyć ile tych wyrazow jest Wiec zobacz a₂ i a₇ sa rowne 0 a wyrazy a₃,a₄ a₅ i a₆ sa mniejszse od zera . Ile jest tych wyrazow ?

Majjjka: 4?

5-latek: Przedzial obliczny masz dobrze (zobacz ze napisaliśmy w jednakowym czasie (14:50

5-latek: tak będą to 4 wyrazy

Majjjka: Ok,wiec to juz koniec tego zadania ?

Majjjka: Super,dziekuje.

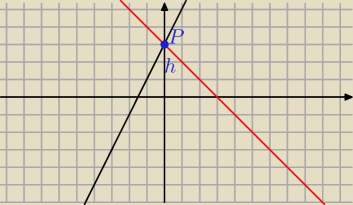
5-latek: Co do zadania nr 4 to należy trochę pomyslec Mamy prosta y= mx+3 gdzie m to wspolczynnik kierunkowy tej prostej i mamy go poszukać gada Prosta ta ma przecina obie osie układu wspolrzednych (osie maja być dodatnie Jeśli narysuje sobie prosta np y=2x+3(czarna to już widzimy ze przy m>0 prosta ta nie przetnie obu osi dodatnich Wiec z tego wynika ze m <0 musi być np. taka y=−x+3 (czerona Tylko z eto nie będzie postac naszsej szukanej prostej Z rysunku widać ze prosta o ujemnym wspolczynniku m przecinając obie osie dodatnie wyznaczy nam trojkat prostokątny Pole tego trojkata ma być rowne 7 Z gimnzajum wiemy ze wspolczynnik b we wzorze funkcji liniowej informuje nas w jakim punkcie wykres funcji przetnie os OY my may taka funkcje y=mx+3 (wiec przetnie w punkcie P= (0,3) Mamy już punkt przecięcia z osia OY Teraz musimy znalezcz punkt Q przecięcia z osia OX o wspolrzednych (x,0) Wiemy z epole trojkata ma być rowne 7 i wzor na pole trojkata jest taki P= 0,5a*h gdzie a to dlugosc boku trojkata h już znamy bo wynosi 3 (odczytane z rysunku No to liczymy dlugosc tego boku

	P		P
P=0,5a*h to 0,5a=		to a= 2		= policz
	h		h

Potem policzmy m

5-latek: Zapomnialem dopisać ze to policzone a będzie wspolrzedna x_owa punktu Q na osi OX natomiast wspolrzedna y_kowa to wiadomo będzie 0

Majjjka: Dziekuje !