Trójkąt podzielono za pomocą symetralnej... Ela: Trójkąt podzielono za pomocą symetralnej jednego z boków na trójkąt i czworokąt. Na czworokącie opisano okrąg o promieniu r. Uzasadnij, że prawdziwa jest nierówność: 0,5R<r, Gdzie R – promień okręgu opisanego na początkowym trójkącie.

===: Bardzo ciekawe zadanko − Skąd je masz?

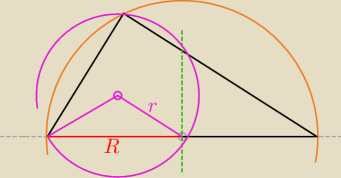
Tadeusz: Skoro czworokąt "odcinany" jest symetralną ... to jeden z jego kątów jest prosty ... a skoro a czworokącie tym można opisać okrąg to i kąt naprzeciw kąta prostego też prosty być musi. Nie ma więc innej możliwości niż taka, że nasz trójkąt jest prostokątny i dzielimy go symetralną przeciwprostokątnej. A dalej to już chyba dostrzegasz nierówność trójkąta 2r>R ⇒ 0,5R<r

Ela: Tak, bardzo ciekawe Takie ćwiczenia napływają na mnie zewsząd Dokładnego źródła niestety nie znam. Dziękuję za pomoc, teraz to zrozumiałam

Tadeusz: −