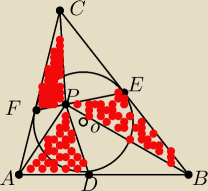
W trójkąt ABC… Ela: W trójkąt ABC wpisano okrąg. Wewnątrz trójkąta obrano punkt P, który połączono za pomocą odcinków z wierzchołkami tego trójkąta oraz z punktami styczności. Trzy z powstałych w ten sposób trójkątów zacieniowano ( na rysunku na czerwono ). Uzasadnij, że iloczyn pól zacieniowanych trójkątów jest równy iloczynowi pól białych ( niezacieniowanych) trójkątów. Pomocy!

Marcin: Nie ma nic więcej? P to jakiś przypadkowy punkt?

Tadeusz:

	1
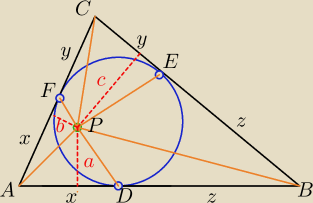
Iloczyn pól trójkątów ADP, CFP i BEP		*xa*yb*zc
	8

	1
Iloczyn pól trójkątów AFP, CEP i BDP		*xb*yc*za i to byłoby na tyle −
	8

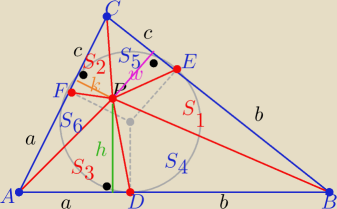Eta: Z tw. o odcinkach stycznych: |AD|=AF|=a , |DB|=BE|=b , |CE|=CF|=c Pola trójkątów czerwonych : S₁, S₂, S₃ Pola trójkątów białych : S₄, S₅, S₆ wspólne ich wysokości to: h, w, k

	w*b		k*c		h*a
S1=		, S2=		, S3=
	2		2		2

	h*b		w*c		k*a
S4=		, S5=		, S6=
	2		2		2

to : S₁*S₂*S₃ = ................. S₄*S₅*S₆ = ................

Eta:

kyrtap:

Ela: Nie Marcin, nic więcej nie było podane Dziękuję

Tadeusz: −