rachunek różniczkowy mikejjla: Proszę o pomoc z rozwiązaniem zadania optymalizacyjnego . Z drutu o długości 1m zbuduj trójkąt prostokątny o największym polu. Znajdź dlugości boków tego trójkąta. a+b+c=1 a²+b²=c² 1=a+b+√a²+b² nie wiem jak z tego równania wyliczyć a lub b, wiem też największe pole będzie miał trójkąt równoramienny, ale nie wiem czy mogę sobie to założyć ...

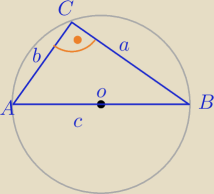Mila: ΔABC− Δprostokątny: a²+b²=c² a+b+c=1

	1
PΔ=		a*b
	2

================= a+b=1−c /² a²+2ab+b²=1−2c+c² 2ab+c²=1−2c+c²⇔2a*b=1−2c c=1−a−b 2a*b=1−2+2a+2b 2a*b=2a+2b−1 2a*b−2b=2a−1 b*(2a−2)=2a−1

	2a−1
b=
	2*(a−1)

	1		2a−1		(2a2−a)
P(a)=		a*		=
	2		2*(a−1)		(a−1)

	2a2−4a+1
P'(a)=
	(a−1)2

	2−√2		2+√2
P'(a)=0⇔2a2−4a+1=0⇔a=		lub a=		>1 zatem∉D
	2		2

	2−√2
W a=		funkcja ma maksimum , pochodna zmienia znak z dodatniego na ujemny przy
	2

przejściu przez ten punkt. b= c= dokończ

mikejjla: dziękuję Mila

Mila: