Proszę o sprawdzenie zadania i ewentualne poprawki Weronika: W pudełku jest 6 piłek czarnych i 6 piłek czerwonych. Losujemy jedną piłkę a następnie z pozostałych drugą. Jakie jest prawdopodobieństwo, że pierwsza z wylosowanych piłek jest czarna(A), jeżeli wiadomo, że druga jest czerwona(B)? P(A/B) = ^P(A∩B)_P(B) P(A∩B)=¹₂* ⁶₁₁=⁶₂₂ P(B)=¹₂*⁵₁₁+¹₂*⁶₁₁ P(A/B)= ⁶₁₁

J:

	1
drugie losowanie w żaden sposób nie wpływa na pierwsze ,czyli P(A) =
	12

Weronika: czemu w takim razie ¹₁₂

J: bo prawdopodobieństwo wylosowania kuli czarnej z pudełka,

	1
w którym jest 12 kul i w tym 6 czarnych wynosi:
	12

J:

	1
ups.... oczywiście: P(A) =
	2

Weronika: a nie ¹₂ ?

Jacek: Ile jest wariacji, w których druga jest czerwona: 6*6+6*5 Ile jest wariacji, w których druga jest czerwona oraz pierwsza jest czarna: 6*6 Teraz to dzielimy i mamy:

6
11

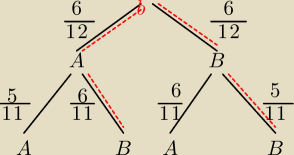
Mila: A− pierwsza wylosowana kula czarna B− druga wylosowana kula czerwona

	1		6		1		5		1
P(B)=		*		+		*		=
	2		11		2		11		2

	1		6		3
P(A∩B)=		*		=
	2		11		11

	3   11		6
P(A/B)=		=
	1   2		11