xzz seta: czy jeżeli dwusieczna dzieli bok na np. x i y, to mogę ułożyć równanie z tw. sinusów? wydaje mi się to dziwne.

x		y
	=		=> x=y?
sinα		sinα

===: a co tu dziwnego? Na przeciwko równych kątów równe boki ... trójkąt równoramienny

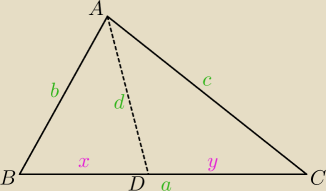
seta: Mam wykazać, że jeśli dwusieczna kąta przy wierzchołku K w trójkącie ABC przecina bok BC w punkcie D, to d²=bc−cx |AB|=b |AC|=c |BC|=a, |BD|=x, |DC|=y

	x		xc
najpierw z tw. dwusiecznej równanie:		={b}{c} ⇒ y=
	y		b

y		x
	=		⇒ y=x ⇒ y={yc}{b} ⇒ c=b.. a w tym co trzeba dowieść b i c są
sinx		sinx

rozróżnialne..

seta: przy wierzchołku A*

seta: no i d=|AD|, czyli owa dwusieczna

seta: ≈≈≈

seta: α

===: piłeś/piłaś coś dzisiaj ? Najpierw wypisujesz jakieś reminiscencje ... teraz "dwusieczna kąta przy wierzchołku K w trójkącie ABC" ... rozumiesz coś z tego ... bo ja nie −:(

seta: nic a nic. wykazać, że jeśli dwusieczna kąta przy wierzchołku A w trójkącie ABC przecina bok BC w punkcie D, to |AD|²=|AB|*|AC|−|AC|*|BD| i z twierdzenia sinusów wychodzi, że |BD|=|DC|, ale to przecież bzdura bo wtedy dwusieczna byłaby tym samym co środkowa...

===: d²=bc−cx

===: twierdzenie sinusów dotyczy kątów w jednym trójkącie JEDNYM ! to że mają jeden bok wspólny i jeden kąt równy przystającymi ich nie czyni

seta: dzięki! o to mi chodziło, bo wydawało mi się to głupotą x) mógłbym w takim razie prosić o jakąś wskazówkę, jak wykonać to zadanie?

===: może z pół trójkątów S_ΔABC=S_ΔABD+S{ΔACD}

seta: z dorysowania wysokości + twierdzenia o współliniowej postawie i tej samej wysokości niestety nic nie wynika.

sin2αbc
	={sinαbd+sinαdc}{2} ⇒ 2sinαcosα=sinαbd+sinαdc
2

	d(b+c)
cosα=
	2

i próbuję przyrównać do tego co wychodzi z tw. cosinusów, ale niebardzo dochodzę do jakichś konkretnych wniosków.

gornix: ^x_y=^b_c − to wynika z tw. o dwusiecznej kata wewnętrznego w trójkącie.

gornix: nie zauważyłem, że jest to już napisane przepraszam

gornix: a w treści zadania nie było, że b=x?