wykazać feint: przez punkt H dzielący wysokosc trapezu ABCD w stosunku m : p poprowadzono prostą równoległą do podstawy AB, która przecina boki BC i AD odpowiednio w punktach K i L. Wykazać, że

	ma + pb
|KL| =		, gdzie a = |AB|, b = |CD|.
	m+p

PPPP: XDD

feint: buuuuuuuuuuuuagaam.

Szef: Narysuj trapez prostokątny. Oznacz odcinek |KL|=c. Poprowadź wysokość tak, aby otrzymać trójkąt z jednej strony trapezu. Jeżeli "c" dzieli wysokość w stosunku (m : p) to tak ta sama wysokość podzieli wysokość w tym trójkąciku. Teraz możesz oznaczyć odcinek środkowy równoległy do "b" i "a" jako różnica : (c−a), a odcinek przy podstawie: (a−b). Jeżeli podzieliłeś wysokość w stosunku: m : p to możesz napisać : m+p= H. Teraz z twierdzenia Talesa układasz stosunek, z którego wyjdzie twoje twierdzenie.

Benny: Nie mogę tego b do równania wrzucić. Spróbowałem tak. Z podobieństwa figury LKCD i ABCD

a−b		|KL|−b
	=
m+p		m

am−bm
	+b=|KL|
m+p

am−bm+bm+pb
	=|KL|
m+p

ma+pb
	=|KL|
m+p

Niby coś wyszło, ale nie jestem przekonany, że mogłem taki myk zrobić.

feint: mogłeś gówno mi zajęło całkiem sporo czasu ;−; wreszcie spokój xd

Benny: Może poczekaj aż ktoś to potwierdzi, bo ja sobie tylko tak dobrałem, żeby się poskracało do odpowiedzi

Benny: Wejdź tu ktoś

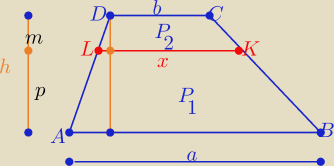
Eta: P₁+P₂= P(trapezu)

a+x		x+b		a+b
	*p+		*m=		(m+p) ⇒
2		2		2

	am+bp
ap+xp+bm+xm=am+ap+bm+bp ⇒ x(m+p)=am+bp ⇒x=|KL|=
	m+p

c.n.w.