pytanie Prezesik: Wielokątem ktorego liczba przekątnych jest 3 razy większa od liczby wierzchołków jest a)kwadrat b)6 kąt wypukly c)8 kąt wypukły d)9 kąt wypukły mam pytanie, jak najszybciej poradzic sobie z tego typu zadaniem, gdy nie pamiętam wzoru na nie? bo rysowanie wszystkich przekątnych 9kąta może być trochę nie czytelne i długie

YushokU: ja zawsze na logikę sobie te wzory wyprowadzałem, a teraz to już anwet pamiętam

yolex: n(n−3)/2

kix:

	n(n−3)
liczba przekątnych
	2

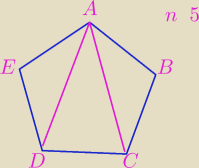
Mila: 1) Sposób z GM. Rysujesz pięciokąt i takie rozumowanie: n=5 Z jednego wierzchołka prowadzisz 2 przekątne , czyli: (n−3) Wierzchołków jest 5. Wzór

(n−3)*n
	, dzielę przez 2 , bo każdą przekątną liczyliśmy dwa razy
2

( z A do C i z C doA) 2) sposób z LO Jeżeli masz n wierzchołków wielokata wypukłego, to możesz utworzyć

n 2		n*(n−1)
	=		odcinków, z tego n jest boków, to przekątnych jest:
		2

n*(n−1)
	−n
2

Mila: Albo podstawiasz po kolei do wzoru, albo rozwiązujesz równanie.

n(n−3)
	=3n, n≥4
2

n*(n−3)=6n n²−3n=6n n²−9n=0 n(n−9)=0 n=9 spr .

n*(n−3		9*6
	=		=27
2		2

27=9*3

Prezesik: dziękuję ślicznie

Mila: Pomogło?