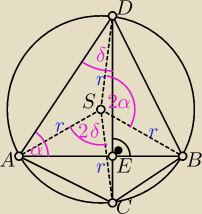
 Długość promienia = r, w trójkącie AED: δ = 90o − α, sinα = cosδ.
Skorzystamy z tożsamości: 1 − cos2x = 2sin2x
Z twierdzenia cosinusów w trójkątach ACS i BSD:
|AC|2 = 2r2 − 2r2cos2δ = 2r2(1 − cos2δ) = 2r2 * 2sin2δ = 4r2cos2α
|BD|2 = 2r2 − 2r2cos2α = 2r2(1 − cos2α) = 2r2 * 2sin2α = 4r2sin2α
|AC|2 + |BC|2 = ...
Długość promienia = r, w trójkącie AED: δ = 90o − α, sinα = cosδ.
Skorzystamy z tożsamości: 1 − cos2x = 2sin2x
Z twierdzenia cosinusów w trójkątach ACS i BSD:
|AC|2 = 2r2 − 2r2cos2δ = 2r2(1 − cos2δ) = 2r2 * 2sin2δ = 4r2cos2α
|BD|2 = 2r2 − 2r2cos2α = 2r2(1 − cos2α) = 2r2 * 2sin2α = 4r2sin2α
|AC|2 + |BC|2 = ...
| |AC| | |BD| | ||
= 2r ⇒ |AC| = 2r cosα i | = 2r ⇒ |BD| = 2r sinα | ||
| sinδ | sinα |